Variables aléatoires
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
par jeje56 » 29 Nov 2008, 10:56
Bonjour,
Soit
Une urne contient une boule rouge et n-1 boules vertes. On effectue des tirages successifs au hasard d'une boule dans l'urne.
Si la boule tirée est rouge, on la remet dans l'urne (avant le tirage suivant); si la boule tirée est verte, on ne la remet pas dans l'urne (avant le tirage suivant).
Soit X la VA qui donne le rang où pour la première fois on a tiré une boule rouge. Déterminer la loi de X.
J'ai fait :
P(X=1)=1/n
P(X=2)=1/(n-1)
P(X=k)=1/(n-k+1)
Cela me parait trop "simple"... Est-ce exact ?
Merci bcp à vous !
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
par nodgim » 29 Nov 2008, 11:42
jeje56 a écrit:si la boule tirée est verte, on ne la remet pas dans l'urne (avant le tirage suivant).
ça veut dire qu'on la remet après le tirage suivant ? :doh: ou alors on ne remet les boules vertes seulement quand on a tiré la boule rouge ?
C'est ambigu.
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
par jeje56 » 29 Nov 2008, 12:01
nodgim a écrit:ça veut dire qu'on la remet après le tirage suivant ? :doh: ou alors on ne remet les boules vertes seulement quand on a tiré la boule rouge ?
C'est ambigu.
"avant de procéder au tirage suivant" autant pour moi...
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
par nodgim » 29 Nov 2008, 12:16
jeje56 a écrit:"avant de procéder au tirage suivant" autant pour moi...
Hum...pas vraiment plus clair...
Tentons avec cette hypothèse
P(x=1)=1/n
P(x=2)=(n-1)/n * 1/(n-1)= 1/n
P(x=3)=(n-1)/n*(n-2)/(n-1)*1/(n-1)= (n-2)/(n(n-1))
P(x=k)=(1/n)*[(n-2)/(n-1)]^(k-2)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
par jeje56 » 29 Nov 2008, 12:33
nodgim a écrit:P(x=3)=(n-1)/n*(n-2)/(n-1)*1/(n-2)
plutôt non ???
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
par jeje56 » 29 Nov 2008, 13:32
J'obtiens alors : P(X=k)=1\n pour tout k...
Cela me parait étrange...
Merci bcp !
-
Isomorphisme
- Membre Naturel
- Messages: 67
- Enregistré le: 09 Aoû 2007, 14:27
-
par Isomorphisme » 29 Nov 2008, 15:17
Bonjour,
Oui je pense que c'est plutôt bizarre ! Essayez plutôt cette formule classique :
 = \mathbb{P} (A_2|A_1) \mathbb{P} (A_3|A_2 \cap A_1) \times ... \times \mathbb{P} (A_k | A_1 \cap ... \cap A_{k-1}) \mathbb{P} (A_1))
où
= "tirer une boule verte" pour
et
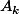
= "tirer une boule rouge"
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
par nodgim » 29 Nov 2008, 15:44
jeje56 a écrit:plutôt non ???
Non, justement!
Tel l'énoncé, la boule verte est remise après le tirage suivant, donc il y a toujours dans l'urne au moins n-1 boules.
Sinon, si on tire les boules vertes et qu'on ne les remet qu'après le tirage d'une boule rouge, le résultat est effectivment 1/n. Mais, ce n'est pas l'énoncé...
-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
par nuage » 29 Nov 2008, 17:55
Salut,
jeje56 a écrit:J'obtiens alors : P(X=k)=1\n pour tout k...
Cela me parait étrange...
Merci bcp !
moi cela me parait juste. En précisant
-
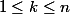
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
par jeje56 » 29 Nov 2008, 18:34
Ok, merci à tous ;-) je reste sur le 1/n.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
