Variables aléatoires indépendantes de même loi que X

[Anna24]

Bonjour,

Il y a une question à laquelle je bloque, je ne vois vraiment pas comment démarrer. J'ai répondu au questions précédentes mais là.. je ne vois absolument pas comment commencer oO

Pourriez vous m'éclairer de vos lanternes s'il vous plait?

Voici l'énoncé:
On considère la variable aléatoire U=INF(T1,T2,T3) définie par:
pour tt t appartenant à R, (U>t)=(T1>t) (T2>t) (T3>t)
a) Montrer que la fct de répartion G de U peut s'écrire:
G(u) = 0 si u<2
G(u)= 1-(2/u)^(3/2) si u supérieur ou égale à 2
b) Montrer alors que U admet une densité g que l'on déterminera


Je bloque dés le début je ne vois pas du tout comment partir.. On a aucun chiffre..oO

Peut être qu'il y a un lien avec les questions précédentes mais je ne vois pas non plus..
Précédemment j'ai traité d'une var X admettant f pour densité en sachant que par hypothèse on avait:
f(x) = 0 Si x<2
f(x)= 1/(x * racine carrée de (2x)) Si x sup ou égal à 2


Merci beaucoup par avance!!

[girdav]

Quelles hypothèses fait-on sur ,, ?

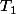
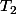
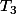
[Anna24]

Bah justement a part ce que j'ai écrit, on ne nous dit rien de plus...
L'énoncé peut être visible ici: http://baudrandmaths.free.fr/exercices/chapitre_VII_vaac.pdf (à partir de la fin de la p18, esc 2003, question 4)

Apparemment il faut revenir à la def de la fct de répartition G: G(t)= P(U inf ou égale à t) = 1 - P(U> t) puis se débrouiller avec ce qu'il y a dans l'énoncé.. mais je ne vois pas...

[girdav]

Tu nous avais caché que ces variables aléatoires sont indépendantes. Dans ce cas on a .

[Anna24]

C'était le titre de mon message ^^ Mais certes je n'avais pas précisé, désolée!

Jusque là j'ai compris merci! Mais après qu'est ce que je fais? J'utilise la définition d'une fct de répartition et donc j'intègre? Mais je vois pas quoi intégrer..? :hein3:

[girdav]

Il suffit de calculer , non?

[Anna24]

ok mais... comment? :s ça doit être évident mais je ne vois pas, normalement la def de P(X inf ou égal à x) = intégrale de - infini à x ....... mais là euh vraiment je vois pas... T1,T2,T3 ou u ne renvoient à un aucun chiffre donc je ne vois pas comment répondre à la question a), c'est peut être simple mais là j'ai vraiment pas compris :triste:

[girdav]

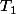
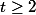
Puisque et ont la même loi, . Ensuite on intègre la densité entre et ; il faut distinguer le cas ou .

[Anna24]

Puisque T1, T2, T3 ont la même loi que X, P(T1 inf ou egale à t) = P(T2 inf ou égale à t) = P(T3 inf ou égale à t) = P( X inf ou égale à t) ??

Donc on a P(U inf ou égale à t) = 1 - (1 - P(X inf ou égale à t) ^3 ?

On calcul P(X inf ou égale à t) en intégrant la densité, mais ici la densité c'est quoi justement? f(x) ? J'ai calculé la fct de répartition de X précédemment, j'ai trouvé 1 qd x sup ou égale à 2 et 0 qd x inf à 2... ça va me redonner pareil si j'intègre encore une fois f(x) ... non?

Donc comment on trouve (2/u) ^3/2? :briques: