Variable aléatoire discrète

[jujudu597]

Bonjour ,

Voici mon problème,

Soit un espace probabilisé et X une variable aléatoire discrète sur . La loi de X sous P est donc



que l'on peut considérer comme proba sur ou sur ou sur .

Cependant, je n'arrive pas à montrer

Jspr que quelqu'un pourras m'aider.

Merci d'avance

[mrif]

Bonjour ,

Voici mon problème,

Soit un espace probabilisé et X une variable aléatoire discrète sur . La loi de X sous P est donc



que l'on peut considérer comme proba sur ou sur ou sur .

Cependant, je n'arrive pas à montrer

Jspr que quelqu'un pourras m'aider.

Merci d'avance

Par définition, pour toute partie de donc:
car la mesure est l'image par l'application de la mesure .

[jujudu597]

Merci de votre réponse.

Mais pourquoi dans ce cas

[mrif]

Merci de votre réponse.

Mais pourquoi dans ce cas

Si tu prends une applicationde dans , avec et , 2 ensembles quelconques alors on a toujours:
.
Si tu n'es pas convaincu essaie de le démontrer, c'est immédiat.

[jujudu597]

Si tu prends une applicationde dans , avec et , 2 ensembles quelconques alors on a toujours:
.
Si tu n'es pas convaincu essaie de le démontrer, c'est immédiat.

Ca n'est vrai qui si f est injective

[jujudu597]

Je crois que je me trompe avec une propriété qui concerne les parties de A et non A tout entier!

Je vais donc y réfléchir!

Merci beaucoup à vous!

[mrif]

Ca n'est vrai qui si f est injective

On est d'accord que
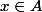
Soit , alors donc ce qui prouve que .
Les 2 inclusions montrent bien que .

[Ben314]

On est d'accord que

Si alors

Et, effectivement, on a pour tout A ssi f est injective

[jujudu597]

Si alors

Et, effectivement, on a pour tout A ssi f est injective

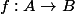
Et donc pour une fonction comment montre t'on que

[Ben314]

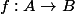
Et donc pour une fonction comment montre t'on que

Si l'ensemble de départ de f c'est A, alors l'image réciproque d'absolument n'importe quelle partie de B est évidement une partie de A !!! (c.f. la définition d'une image réciproque)

[jujudu597]

Merci beaucoup! :)

[mrif]

Si alors

Et, effectivement, on a pour tout A ssi f est injective

Sauf que A n'est pas une partie quelconque, mais l'ensemble de départ de l'application f.