bonsoir
je voudrais démontrer la formule de Legendre pour n! ,en rapport avec la valuation de n !
merci encore
Valuation de n!
6 messages
- Page 1 sur 1
par lapras » 09 Juin 2008, 21:10
Salut
cette formule -bien qu'impressionante- est tres facile à montrer
pour avoir le nombre de nombre dans n! (parmis 1 , 2 , 3 , ... , n) dont la valuation p adique est 1 il faut calculer :
[n/p] - [n/p²] - [n/p^3] - .....
car il y a p multiples de p <= à n mais on compte aussi ceux dont la valuation p adique est 2 , 3 , .. donc il faut les décompter (d'où le - [n/p²] - [n/p^3] -...)
de même pour le nombre de nombre dont la valuation p adique est exactement 2 : [n/p²] - [n/p^3] - ....
sauf qu'on va ajouter un facteur 2 au [n/p²] car la valuation p adique est = 2 et comme on cherche la valuation p adique totale de n!, il faut ce facteur 2.
de même on continue
donc la valuation p adique de n! est :
([n/p] - [n/p²] - [n/p^3] - [n/p^4] - .... ) + (2*[n/p²] - [n/p^3] - [n/p^4]....) + (3*[n/p^3] - [n/p^4] - ......) = [n/p] + [n/p²] + [n/p^3] + .....
cette formule -bien qu'impressionante- est tres facile à montrer
pour avoir le nombre de nombre dans n! (parmis 1 , 2 , 3 , ... , n) dont la valuation p adique est 1 il faut calculer :
[n/p] - [n/p²] - [n/p^3] - .....
car il y a p multiples de p <= à n mais on compte aussi ceux dont la valuation p adique est 2 , 3 , .. donc il faut les décompter (d'où le - [n/p²] - [n/p^3] -...)
de même pour le nombre de nombre dont la valuation p adique est exactement 2 : [n/p²] - [n/p^3] - ....
sauf qu'on va ajouter un facteur 2 au [n/p²] car la valuation p adique est = 2 et comme on cherche la valuation p adique totale de n!, il faut ce facteur 2.
de même on continue
donc la valuation p adique de n! est :
([n/p] - [n/p²] - [n/p^3] - [n/p^4] - .... ) + (2*[n/p²] - [n/p^3] - [n/p^4]....) + (3*[n/p^3] - [n/p^4] - ......) = [n/p] + [n/p²] + [n/p^3] + .....
par road runner » 09 Juin 2008, 21:38
j'avoue que je n'ai pas très bien compris ,un peu plus d'aide svp ?
par Aspx » 10 Juin 2008, 17:00
Une démonstration de cette formule utilise une matrice d'adjacence.
On fixe un entier
quelconque et on recherche la valuation p-adique (notée
) de
.
Soit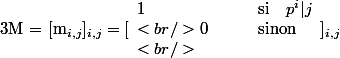
. Calculons de deux manières différentes la somme de tous ses éléments.
Déjà à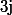
fixé on a, vu que }|j)
et +1})
ne divise pas 
[CENTE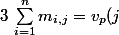R])
[/CENTER]
Puis
[CENTER]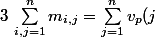 = v_p(\prod_{j=1}^{n} j) = v_p(n!))
[/CENTER]
Ensuite si on fixe
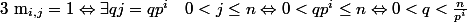
Il y a donc)
valeurs possibles pour q. Il s'en suit le résultat connu en sommant sur
[CENTER] = \sum_{k=1}^{n} E(\frac{n}{p^k}))
[/CENTER]
On fixe un entier
Soit
Déjà à
[CENTER]
Puis
[CENTER]
Ensuite si on fixe
Il y a donc
[CENTER]
par aviateurpilot » 10 Juin 2008, 17:59
autre solution:
=v_p(\bigprod_{k=1}^{[n/p]}kp))
(car =v_p(a))
si =1)
donc dans le produit 1x2x....xn on laisse seulement les multiples de )
donc=v_p(p^{[n/p]}[n/p]!)=[n/p]+v_p([n/p]!))
et de meme pour=\[\frac{\[\frac{n}{p^{k}}\]}{p}\]+v_p(\[\frac{\[\frac{n}{p^{k}}\]}{p}\]!))
et on a
d'ou=v_p(n!)-v_p([n/p])+\fbox{\bigsum_{k=1}^{+\infty}v_p\(\[\frac{n}{p^{k+1}}\]\)-v_p\(\[\frac{n}{p^k}\]\)}=\bigsum_{k=1}^{n}\[\frac{n}{p^k}\])
donc
et de meme pour
et on a
d'ou
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :