Bonjour,
Soit f une endomorphisme de E de dimension finie avec f différent de id et f différent de 2id vérifiant
(f-id)°(f-2id)=0
1/ Quelles sont les valeurs propres de f ?
2/ Si f diagonalisable, comment affiner le raisonnement du 1/ ?
1/ J'ai fais la 1 ère question en disant qu'un polynôme annulateur était P(X)=(X-1)(X-2). Donc les valeurs propres possibles sont 1 et 2.
2/ Je n'arrive pas à faire cette question car on ne connaît pas la dimension de E et je n'ai pas assez d'éléments pour avancer.
Merci d'avance pour vos réponses.
Valeur propre de f
9 messages
- Page 1 sur 1
Re: valeur propre de f
Tout d'abord, on dit un endomorphisme (et pas une).
Si tu as compris mon explication sur ta question précédente, tu devrais pouvoir utiliser le polynôme minimal de pour déterminer les valeurs propres de
pour déterminer les valeurs propres de  .*
.*
La question 2 est bizarre. Vu l'hypothèse faite, est forcément diagonalisable.
est forcément diagonalisable.
*Soit le polynôme minimal de
le polynôme minimal de  et soit
et soit  une racine de
une racine de  . On a donc
. On a donc 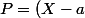Q) .
.
Si n'était pas une valeur propre de
n'était pas une valeur propre de  ,
,  serait inversible et on aurait
serait inversible et on aurait =(f-a\,\mathrm{Id}_E)^{-1}P(f)=0) , donc
, donc  ne serait pas le polynôme minimal de
ne serait pas le polynôme minimal de  .
.
Si tu as compris mon explication sur ta question précédente, tu devrais pouvoir utiliser le polynôme minimal de
La question 2 est bizarre. Vu l'hypothèse faite,
*Soit
Si
Re: valeur propre de f
GaBuZoMeu a écrit:Tout d'abord, on dit un endomorphisme (et pas une).
Si tu as compris mon explication sur ta question précédente, tu devrais pouvoir utiliser le polynôme minimal depour déterminer les valeurs propres de
.*
La question 2 est bizarre. Vu l'hypothèse faite,est forcément diagonalisable.
*Soitle polynôme minimal de
et soit
une racine de
. On a donc
.
Sin'était pas une valeur propre de
,
serait inversible et on aurait
, donc
ne serait pas le polynôme minimal de
.
Effectivement un endomorphisme
Je ne vois pas le rapport entre le polynôme minimal et les valeurs propres sauf que le polynôme minimal divise un des polynôme annulateur de f.
Donc Pmin est de la forme (X-1)*Q ou (X-2)*Q ou (X-1)(X-2)*Q et donc après ?
Et pourquoi f est forcément diagonalisable ?
Merci pour votre réponse.
Re: valeur propre de f
Tu as visiblement une mauvaise compréhension de ce qu'est le polynôme minimal d'un endomorphisme  .
.
As-tu bien vu cette notion dans ton cours ?
Quelle est la définition du polynôme minimal d'un endomorphisme ?
As-tu bien vu cette notion dans ton cours ?
Quelle est la définition du polynôme minimal d'un endomorphisme ?
Re: valeur propre de f
Bonjour,
je ne crois pas que le polynôme minimal soit au programme (malheureusement ...)
je ne crois pas que le polynôme minimal soit au programme (malheureusement ...)
Re: valeur propre de f
Je n'est pas vu dans le cours cette notion mais je sais que le polynôme minimal divise un des polynômes annulateurs de f mais je ne suis pas assez calé dessus 

Re: valeur propre de f
Le polynôme minimal est un polynôme annulateur qui divise tous les autres polynômes annulateurs. C'est un polynôme annulateur de degré minimal, et il est unique à multiplication par une constante près.
On peut traiter l'exercice sans cette notion.
Montre dans un premier temps que les seules valeurs propres possibles sont 1 et 2
Montre ensuite que si 1 n'est pas valeur propre, alors f=2Id.
Je ne comprends toujours pas la question 2 de l'exercice. Elle me semble complètement loufoque.
On peut traiter l'exercice sans cette notion.
Montre dans un premier temps que les seules valeurs propres possibles sont 1 et 2
Montre ensuite que si 1 n'est pas valeur propre, alors f=2Id.
Je ne comprends toujours pas la question 2 de l'exercice. Elle me semble complètement loufoque.
Re: valeur propre de f
A mon avis la question 2 est l'ajout malencontreux d'un professeur qui a voulu rajouter sa patte à l'exo...
Mais comme GBZM l'a dit, 1) ce cas n'arrive jamais et 2) la question "affiner le raisonnement" n'a pas de sens mathématique précis
Mais comme GBZM l'a dit, 1) ce cas n'arrive jamais et 2) la question "affiner le raisonnement" n'a pas de sens mathématique précis
Re: valeur propre de f
GaBuZoMeu a écrit:Le polynôme minimal est un polynôme annulateur qui divise tous les autres polynômes annulateurs. C'est un polynôme annulateur de degré minimal, et il est unique à multiplication par une constante près.
On peut traiter l'exercice sans cette notion.
Montre dans un premier temps que les seules valeurs propres possibles sont 1 et 2
Montre ensuite que si 1 n'est pas valeur propre, alors f=2Id.
Je ne comprends toujours pas la question 2 de l'exercice. Elle me semble complètement loufoque.
J'ai rien compris moi aussi à la question 2.
Pour en venir à la question 1, si j'ai bien compris 1 et 2 sont les possibles valeurs propres de f.
On raisonne par l'absurde après, c'est ça ?
Si 1 n'est pas valeur propre alors f=2id pas possible donc 1 est valeur propre
Si 2 n'est pas valeur propre alors f=id pas possible donc 2 est valeur propre
Merci
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
