Valeur moyenne
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
par aure555 » 08 Mai 2008, 13:40
Bonjour, voici l'énoncé :
Soit X une variable aléatoire et F la fonction de répartition
 = \left\{ 0 \qquad pour x < 0 \\ \frac{1}{2} x^2 \qquad pour 0 \leq x < 0.4 \\ \frac{1}{4}+\frac{1}{2}x^2 \qquad pour 0.4 \leq x < 0.6 \\\frac{1}{2}+\frac{1}{2}x^2 \qquad pour 0.6 \leq x < 1 \\ 0 \qquad pour x \geq 1)
Il faut calculer la valeur moyenne E(x).
Pour celà je calcule donc la dérivée de
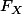
pour avoir la densitée de probabilité f et pouvoir calculer la valeur moyenne de la manière suivante :
 = \int_{-\infty}^{+\infty} x f(x) dx)
 = \left\{ 0 \qquad pour \, x < 0 \\ x \qquad pour \, 0 \leq x < 1 \\ 0 \qquad pour \, x \geq 1)
On a donc
 = \int_{0}^{1} x^2 dx = \frac{1}{3})
...
La réponse qu'il nous avait été donné est de
.
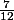
Pourriez-vous m'indiquer où mon raisonnement est incorrect?
Merci
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
par Quidam » 08 Mai 2008, 14:18
aure555 a écrit:Bonjour, voici l'énoncé :
Soit X une variable aléatoire et F la fonction de répartition
Il faut calculer la valeur moyenne E(x).
Pour celà je calcule donc la dérivée de
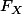
pour avoir la densitée de probabilité f et pouvoir calculer la valeur moyenne de la manière suivante :
On a donc
...
La réponse qu'il nous avait été donné est de
.
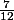
Pourriez-vous m'indiquer où mon raisonnement est incorrect?
Merci
Tes trois dérivées sont tout simplement fausses ! Recommence !
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
par Quidam » 08 Mai 2008, 14:20
Comment expliquer que la fonction de répartition soit discontinue ? Réfléchis à ce que cela signifie !
P.S. D'ailleurs, F(x)=1 pour x > 1 !
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
par aure555 » 08 Mai 2008, 14:57
Quidam a écrit:P.S. D'ailleurs, F(x)=1 pour x > 1 !
Pourrais-tu explicité plus? parce que on a définit F(x) = 0 pour x
1
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
par Quidam » 08 Mai 2008, 15:11
aure555 a écrit:Pourrais-tu explicité plus? parce que on a définit F(x) = 0 pour x
1
Ce n'est pas possible, c'est une erreur ! La fonction de répartition est par définition croissante. Elle croît de 0 à 1.
=0)
et
=1)
Si P(X>1)=0 alors, nécessairement, F(1)=1 et F(x)=1 pour tout x>1
Si P(X<0)=0 alors, nécessairement, F(0)=0 et F(x)=0 pour tout x<0
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
par aure555 » 08 Mai 2008, 15:29
Ok merci pour ton explication clair j'ai compris. Je vais donc modifier l'énoncé et me repencher sur le problème en tenant compte de ta remarque ci-dessus
Merci
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
par aure555 » 08 Mai 2008, 21:12
Dans une correction qui nous a été fourni on calcul l'intégrale de la façon suivante :
 + \int_{]0.4-0,0.4]}x dF(x) + \int_{]0.4,0.6-0]}x dF(x) + \int_{]0.6-0,0.6]}x dF(x) + \int_{]0.6,1]}x dF(x))
mais je ne vois pas à quoi sert la décomposition par exemple avec ]0.4-0,0.4].
Pour les 1er, 3ème et 5ème termes, la correction donne le résultat de
comme calculé en haut.
Ensuite pour le 2ème terme le calcul de l'intégrale donne
 = 0.4[F(0.4)-F(0.4-0)] = 0.4[\frac{1}{4} + \frac{1}{2}(0.4)^2 - \frac{1}{2}(0.4)^2] = \frac{1}{10})
J'ai du mal à comprendre ce calcul.
Pourquoi distinguer 0.4 et 0.4-0??
Merci
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
par Quidam » 08 Mai 2008, 22:29
Lorsque l'on est en présence d'une densité de probabilité f(x) sur un intervalle, la probabilité
)
est voisine de
\times \varepsilon)
. Pour
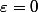
, la probabilité en question est nulle. Mais si la fonction de répartition n'est pas continue en 0.4, cela signifie que la probabilité P(X=0.4) n'est pas nulle. Elle est égale à
-F(0.4-\varepsilon))
, c'est-à-dire à la discontinuité de F en 0.4.
Donc, tu dois considérer que la loi de probabilité est à la fois discrète pour certains points et à densité de probabilité pour certains intervalles.
=\int_0^{0.4} xf(x)dx+0.4\ P(X=0.4)+\int_{0.4}^{0.6} xf(x)dx+0.6\ P(X=0.6)+\int_{0.6}^{1} xf(x)dx)
Avec P(X=0.4) = discontinuité de F en 0.4
et P(X=0.6) = discontinuité de F en 0.6
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
par aure555 » 09 Mai 2008, 09:45
Ah ok d'accord j'ai compris le principe.
Ton explication est clair et limpide
Merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
