Valeur approchée

par **Near** » 30 Jan 2010, 17:24

salut
soit la fonction suivante

.
déterminer une valeur approchée de

et de

à l'aide de la valeur de

en

.
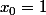
pour la dérivé,

quelle formule dois-je utiliser pour trouver les valeurs approchées ?
merci.

par **alavacommejetepousse** » 30 Jan 2010, 17:38

bonsoir

utilise un dl à l'ordre 1

f(1+h) est peu différent de f(1)+hf ' (1) pour h petit

le problème est que tu ne controles pas l'erreur commise

une formule de taylor à l'ordre 1 avec une majoration de l f " l sur [a,b] serait plus précise

par **Near** » 30 Jan 2010, 19:27

merci :we:
donc,

.
est-ce ça ?

par **alavacommejetepousse** » 30 Jan 2010, 22:21

Near a écrit:merci :we:
donc,
.
est-ce ça ?

l'avant dernier signe d'égalité est abusif mais je présume que c'est la valeur numérique approchée demandée.

par **Near** » 31 Jan 2010, 14:52

alavacommejetepousse a écrit:l'avant dernier signe d'égalité est abusif mais je présume que c'est la valeur numérique approchée demandée.

merci beaucoup.

Valeur approchée

valeur approchée

Qui est en ligne