Valeur d'adhérence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nelloune
- Membre Naturel
- Messages: 51
- Enregistré le: 13 Mar 2019, 00:25
-
 par nelloune » 10 Juin 2019, 17:45
par nelloune » 10 Juin 2019, 17:45
Bonsoir ,
Je bloque sur le calcul des valeur d'adhérence de la série suivante:
bn=(1-
^n}{n})
)^
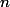
Merci d'avance
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 10 Juin 2019, 18:01
par GaBuZoMeu » 10 Juin 2019, 18:01
Peux-tu étudier les sous-suites des termes de rang pair et de rang impair ?
-
mathelot
 par mathelot » 10 Juin 2019, 18:25
par mathelot » 10 Juin 2019, 18:25
bonjour,
la série est à termes positifs. Comme elle diverge grossièrement (son terme général ne tend pas vers zéro)
on en déduit la ou les valeurs d'adhérence sans calcul
-
nelloune
- Membre Naturel
- Messages: 51
- Enregistré le: 13 Mar 2019, 00:25
-
 par nelloune » 10 Juin 2019, 18:30
par nelloune » 10 Juin 2019, 18:30
D'accord mais si j'etudie les sous-suites des termes de rang pair et impair ça marche aussi ?
-
mathelot
 par mathelot » 10 Juin 2019, 18:38
par mathelot » 10 Juin 2019, 18:38
oui, sans doute
-
nelloune
- Membre Naturel
- Messages: 51
- Enregistré le: 13 Mar 2019, 00:25
-
 par nelloune » 10 Juin 2019, 18:41
par nelloune » 10 Juin 2019, 18:41
D'accord merci
-
aviateur
 par aviateur » 10 Juin 2019, 18:47
par aviateur » 10 Juin 2019, 18:47
Bonjour
Je pense que tu veux dire valeurs d'adhérences de la suite
)
(et non de la série
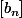
)
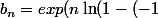^n/n)))
^n/n))=exp(n (-(-1)^n/n +o(1/n))= exp(-(-1)^n +o(1)))
(vient de ln(1+u)=u+o(u) quand u tend vers 0)
La suite
)
ne converge pas
mais si n=2 p (i.e si n est pair)
))
tend vers exp(-1)
tandis que si n=2 p+1 (i.e si n est impair)
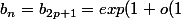))
tend vers
)
La suite admet donc 2 valeurs d'adhérences exp(1) et exp(-1)
Modifié en dernier par aviateur le 10 Juin 2019, 19:06, modifié 1 fois.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 10 Juin 2019, 19:02
par GaBuZoMeu » 10 Juin 2019, 19:02
J'avais lu "suite" alors qu'il y a écrit "série".
C'est "série" ou "suite" dans le vrai énoncé ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités