Bonsoir
J’aurais besoin de votre aide pour résoudre un exercice.
L’énoncé est le suivant :
Déterminer l’ensemble des (x,y) dans R tels que :
2 abs(xy) = x2 + y2
Abs signifie valeur absolue, x2 = x au carré
J’imagine qu’il faut analyser le signe de xy mais je crois que je manque de méthode pour résoudre l’exercice. Pouvez-vous m’aider ?
Je vous en remercie.
Joquetino
Valeur absolue et équations second degré
7 messages
- Page 1 sur 1
Re: Valeur absolue et équations second degré
Est-ce que tu sais résoudre l'équation 
Ce sera de toutes façons une des étapes de l'exercice.
Résous cette équation, et ensuite, il faudra voir ce qu'il reste à faire pour finir l'exercice. Ca, c'est à faire sur ta feuille de brouillon. Sur la copie à remettre au prof, il faudra sûrement 'habiller' un peu mieux le raisonnement.
Ce sera de toutes façons une des étapes de l'exercice.
Résous cette équation, et ensuite, il faudra voir ce qu'il reste à faire pour finir l'exercice. Ca, c'est à faire sur ta feuille de brouillon. Sur la copie à remettre au prof, il faudra sûrement 'habiller' un peu mieux le raisonnement.
Re: Valeur absolue et équations second degré
Bonjour
on a déjà x=0 , y=0 comme solution
aucune solution si x=0 et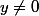
aucune solution si y=0 et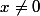
il reste deux cas à voir
le premier cas xy>0
l'équation s'écrit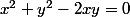
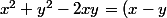^2)
^2=0) donc solution pour tout x =y
donc solution pour tout x =y
le deuxième cas xy<0
l'équation s'écrit
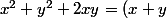^2)
^2=0) solution uniquement avec x=0 et y=0
solution uniquement avec x=0 et y=0
on a déjà x=0 , y=0 comme solution
aucune solution si x=0 et
aucune solution si y=0 et
il reste deux cas à voir
le premier cas xy>0
l'équation s'écrit
le deuxième cas xy<0
l'équation s'écrit
Re: Valeur absolue et équations second degré
hi
n'a-t-on pas
^2 = x^2 + y^2 - 2|xy|)
au quel cas, on cherche juste (x,y) tq |x|-|y| = 0
n'a-t-on pas
au quel cas, on cherche juste (x,y) tq |x|-|y| = 0
la vie est une fête 
Re: Valeur absolue et équations second degré
Effectivement c’est plus simple.
On arrive aux couples (x,-x) et (x,x) avec x appartenant au réel
Je peux conclure de cette façon ?
Merci
On arrive aux couples (x,-x) et (x,x) avec x appartenant au réel
Je peux conclure de cette façon ?
Merci
Re: Valeur absolue et équations second degré
je concluerais de cette façon en tout cas 
la vie est une fête 
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
