Urne, variables aléatoires

[Anonyme]

Bonjour !
Voilà g le début de ce problème qui me pose déja quelques difficultés. Pourriez vous m'aidez afin que je puisse continuer.

Ds tt le problème, r désigne un entier vérifiant 1<= r=>10
Une urne contient 10 boules distinctes B1, B2,...,Br. Une experiance aléatoire consiste à y effectuer une suite de tirages d'une boule avc remise, chaque boule ayant la meme proba de sortir à chaque tirage.
On suppose que le nombre de tirages nécessaires pr obtenir au moins une fois chacune des boules B1,...Br définit une variable aléatoire Yr

1/ On suppose que r =>2. Calculer la proba pr que les r boules B1,...Br sortent dans cete ordre aux r premiers tirages. EN déduire la proba P((Yr=r)) . Préciser l'ensemble des valeurs que peut prendre la variable aléatoire Yr.

2/ Pour tout entier i vérifiant 1<=i>=r, on désigne par Wi la variable aléatoire représentant le nombre de tirages nécessaires pour que, pour la 1ere fois, i boules distinctes parmi les boules B1,...Br soient sorties (en part on a Wr=Yr). On pose X1=W1 et pour tout i vérifiant 2<=i>=r, Xi=Wi - W(i-1). On admet que les vairables aléatoires Xi...Xr sont indépendantes.
Exprimer la variable aléatoire Yr à l'aide des variables aléatoires X1...Xr. Interpreter concretement la variable aléatoire Xi . Montrer que la variable aléatoire Xi suit une loi géo

A la toute premier question g toruvée la proba = (1/10)puissance r
puis que p(Yr=r) suit une loi géométrique de paramètre (1/10)puissance r avec comme ensemble de valeurs [r,n] mais je ne suis vrémen pas sure.
Pour tte la suite je bloque, or j'en ai vrémen besoin pr faire les 10 questions encore restantes. Pourriez vous m'aider. Merci bcp d'avance

[Galt]

Je ne suis pas d'accord
Il ya r boules dans l'urne, donc la proba que les boules sortent dans cet ordre est
Pour un ordre quelconque, on a possibilités, donc une proba de

La variable peut prendre toutes les valeurs entières supérieures ou égales à r

Vu les définitions, on a

En ajoutant ces égalités, on obtient

Et comme ...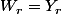

Interprétons
est le nombre de coups pour sortir pour la première fois i boules différentes, et le nombre de coups pour sortir pour la première fois i-1 boules différentes. est donc le nombre de coups où on a attendu la nouvelle boule, elle suit donc une loi géométrique de paramètre (puisque la probabilité qu'une nouvelle boule sorte est ...

[Anonyme]

merci d'avoir regardé !!
mais je ne comprends pas certains points de ton raisonnement. Car en fait tu dis qu'il ya r boules ds l'urne, or l'énoncé di kil yen a 10 et que dans ces 10 on en choisis r je crois.
Quant a la question sur les Wi je ne comprend spas ton raisonnement et ou sa nous ammene.
Merci beaucoup en tout cas de m'aider

[Chimerade]

...or l'énoncé di kil yen a 10 et que dans ces 10 on en choisis r je crois.

Ben, faudrait voir à vérifier ça. Il n'est pas étonnant qu'il y ait mauvaise interprétation de l'énoncé si ton énoncé n'est pas cohérent. Je cite :

Ds tt le problème, r désigne un entier vérifiant 110
Une urne contient 10 boules distinctes B1, B2,...,Br.

Il fallait dire :
[INDENT]Dans tout le problème, r désigne un entier vérifiant 1 m'est inconnu.

2) Si c'était >= ce n'était pas bon non plus, car on ne peut pas écrire : x = z ! Donc je suppose que tu voulais dire <= (je sais bien que <= n'existe pas davantage, mais c'est d'un usage suffisamment courant dans ce forum pour exclure tout ambiguïté). Donc 1<=r<=10

3) Si tu dis "10 boules : B1, B2,... Br", le moins que l'on puisse dire c'est que ptèt ben que r=10 !

Bref ! En résumé, une fois de plus (je sais que ce n'est pas toujours toi !) une question est venue ambiguë, et je répète donc une fois de plus qu'il faut relire ses questions avant de les poster : cela fera économiser du temps à tout le monde !

Cela dit, si j'ai bien compris la question malgré ces incohérences, la réponse à la première question est effectivement

C'est la probabilité que les r boules nommées sortent dans cet ordre. Quelle est donc la probabilité qu'elles sortent dans un autre ordre ? Et combien y a-t-il d'ordres possibles pour r boules ? Conclue !