bonjour chers amis,
ca fait un jour que je me bloque dans un exercice d'equations differentielles. J'ai a resoudre une eq diff, en utilisant les series entieres, donc j'ai a remplacer y pas la somme de 0 a l'infini de CnX^n et puis manipuler un peu les indices, puis identifier y et les constantes. bref. j'essaie de trouver une forme generale des Cn en fonction de C0 et de leurs indices (peut etre en prenant les indices pairs et impairs, mais j'ai tout essayé). Ils sont comme suit:
C0 inconnue (constante arbitraire)
C1=1
C2=1/2 C0
C3=2/3
C4=3/8 C0
C5=8/15
C6=5/16 C0
C7=16/35
C8=35/128 C0
C9= 128/315
C10= 63/256 C0
La formule de recurrence est C(k+1)=C(k-1) x k/(k+1) . Mais il faut que je trouves une forme generale liant les Cn a leurs indices et a C0.
merci bcp
Urgent Recurrence/series entieres/eq diff
4 messages
- Page 1 sur 1
Re: urgent Recurrence/series entieres/eq diff
je te donne la résolution de ta récurrence mais je ne sais pas quoi en faire:
!}{2^{2n}(n!)^2})
^2}{(2n+1)!})
Re: urgent Recurrence/series entieres/eq diff
merci bcp.. je n'ai aucun clou concernant comment j'allais deviner tout cela
Re: urgent Recurrence/series entieres/eq diff
C'est facile:
Par exemple tu calcules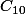 :
:
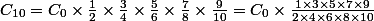
Ensuite tu combles les vides:
Tu mets 2 en facteur dans chaque nombre du dénominateur

Tu symbolises:^2})
Tu généralises sans démonstration:!}{2^{2n}(n!)^2})
Par exemple tu calcules
Ensuite tu combles les vides:
Tu mets 2 en facteur dans chaque nombre du dénominateur
Tu symbolises:
Tu généralises sans démonstration:
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
