Urgent DM pour lundi : sur le vocabulaire d'ensemble

[kaw]

il faut dire si les application suivantes son injective, surjectives ou bijective, et si elles sont bijectives donner leur bijection reciproque

g : R*+ ==> R
x ==> racine(x) - 1/(racine(x))


k : R² ==> R²
(x,y) ==> (x²-y²;xy)


je sais que la première est bijective mais je ne sais pas du tout comment m'y prendre pour rediger et resoudre tout ça :S

[arnaud32]

concernant g:
pour montrer l'injectivite il suffit de montrer que la fonction est stricement monotone
pour la surjectivite, elle est continue et tu donnes ses limites en +oo et 0.
pour la fonction reciproque tu resoud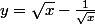
tu vas trouver une equation du second degr en x. avec potentiellemnt deux solutions.
n'oublie pas que y=sign(y)|y|

concernant k:
que penses tu de k(-x,-y)
peux tu resoudre le systeme
x²-y²=a
xy=b

[kaw]

pour la g jessyae de resoudre y=racinex _1/racinex mais je ny arrive pas enfin jarrive a trouver deux solution en fonction de y et je doi en eliminer une selon les condition que jai posé jai resolu dans le cas ou x>1 et y>0 et dans le cas ou x<1 et y<0 , mais je narrive pas a garder un seul des resultat. pasque quand je trace la courbe de lapplication g je trouve quelle est bijective

[arnaud32]

tu as en effet deux solutions en effet.
par contre tu as des conditions aux limite pour y -> +oo et y->-oo
donc il faut que tu choisisses pour x en fonction du signe de y ...

[kaw]

mercii pour la g jy suis arrivé

mais pour la k
en resolvant le systeme je trouve :
b²-y^4=ay²
x=b/y


et je bloque a ce niveau la, quand jessaye de retrouver y ej n'y arriive pas

[arnaud32]

equation du second degre en y ...

[kaw]

alor je trouve
delta = a²+4b²

dou y² = (-a+racine(a²+4b²)) / 2
ou y² = (-a-racine(a²+4b²)) /2


et on a le deuxième cas qui est pas possible par ce que c'est négatif et un carré n'est jamais négaif c'est cela?

[arnaud32]

tu cherche a savoir s'il ya une solution au moins (pour la surjectivite)
l'injectivite, c'est clair que k ne l'est pas car k(x,y)=k(-x,-y)