Bonjour à tous,
Voilà mon énoncé,
[CENTER]Soit E un espace vectoriel normé de dimension finie.
Soit A,B deux ensembles connexes inclus dans E.
Montrer que C = l'union des segments joignant deux points arbitraires de A et B est connexe.[/CENTER]
Je sais qu'un segment dans R est connexe mais que dire d'un segment dans un ev de dim finie ?
J'ai tenté de montrer que C était connexe par arc mais en vain (je n'ai pas l'hypothèse de connexité par arc pour A, B)
De plus je ne sais pas si je peux considérer que l'union des points de A est dénombrable.
Quelqu'un aurait-il une piste siouplé ?
Merci d'avance.
Union de segments connexe
5 messages
- Page 1 sur 1
Bonjour,
oui, un segment d'un e.v. en général est connexe :b;t\in[0;1]\}) .
.
Tu peux montrer que C est connexe par arc, en effet si\in C^2) alors plusieurs cas :
alors plusieurs cas :
1)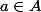 et
et 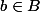 (ou le contraire) alors le segment
(ou le contraire) alors le segment  fait partie de
fait partie de  donc pas de problème.
donc pas de problème.
2) et
et  sont tous les deux dans le même ensemble (par exemple
sont tous les deux dans le même ensemble (par exemple  ) alors on choisit
) alors on choisit  et les segments
et les segments 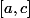 et
et  sont dans
sont dans  et le chemin obtenu par concaténation de ces deux segments est alors dans
et le chemin obtenu par concaténation de ces deux segments est alors dans  .
.
3) Ni ni
ni  ne sont dans
ne sont dans 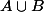 mais ils sont alors sur des segments :
mais ils sont alors sur des segments :  et
et  avec
avec \in A^2) et
et \in B^2) ce qui permet de relier
ce qui permet de relier  et
et  par un chemin dans
par un chemin dans  .
.
oui, un segment d'un e.v. en général est connexe :
Tu peux montrer que C est connexe par arc, en effet si
1)
2)
3) Ni
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
