bonjour
démontrez que l'union de deux dénombrable est dénombrable
et merci d'avance
Union de deus dénombrable
3 messages
- Page 1 sur 1
par Miya » 01 Oct 2007, 01:35
Salut,
On revient à la définition : soit U et V deux dénombrables, alors il existe des bijections entre les éléments de U et de
, et V et . Alors on peut numéroter les ensembles : U = {
, n
} et V = {
, n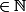
}.
On va créer notre bijection entre U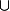
V et ainsi : pour nA, avec 
A
, on associe si n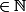, ] et si 
on associe 
pour n<0. On vérifie que c'est une bijection...
Tout est bon, puisque A est dénombrable en tant qu'ensemble compris entre deux ensembles dénombrables.
Voilà voilà, une démonstration bien lourde pour un truc très simple, mais plus c'est simple et plus il faut mettre de la sauce ^^.
Bonne soirée
On revient à la définition : soit U et V deux dénombrables, alors il existe des bijections entre les éléments de U et de
On va créer notre bijection entre U
Tout est bon, puisque A est dénombrable en tant qu'ensemble compris entre deux ensembles dénombrables.
Voilà voilà, une démonstration bien lourde pour un truc très simple, mais plus c'est simple et plus il faut mettre de la sauce ^^.
Bonne soirée
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :