seriousme a écrit:Mais pourquoi ce calcul est faux :
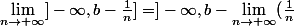] = ]-\infty, b])
?
Parceque tu sembles croire qu'il existe une notion de "limite" ensembliste, donc déjà tu sais pas toi-même de quoi tu parles, et pire, tu crois qu'il y aurait un miracle qui ferait que "x -> [a ; x]" serait une fonction continue de R dans un bidule qui serait une sorte d'espace d'intervalles ou je ne sais quoi compatible avec tes "limites". Donc voilà pourquoi tu as des résultats incohérents.
Donc comme le dit SimonB, évite de vouloir faire des "calculs" sur des trucs que tu n'as même pas définis.
On pourrait interpréter la limite d'une suite décroissante d'ensembles comme l'intersection de tous ces ensembles en même temps, ainsi que la limite d'une suite croissante comme la réunion.
Déjà là, en remplaçant les limites par des unions ou des intersections, tu peux savoir au moins de quels ensembles tu parles. Et ensuite, montrer que 2 ensembles sont égaux ça se fait pas en calculant mais avec un raisonnement.