Bonjour à tous,
Voici mon énoncé,
Soit E un evn.
Soient A,B dans E tels que A et B convexes.
Montrer que l'union des segments joignant deux points arbitraires de A et B est convexe.
(j'avais déjà eu ce problème avec la connexité).
On a X convexe qlq soit x,y dans X, [x,y] est dans X.
Je visualise bien comment procédé et sur quoi je dois retomber.
Voici comment je m'y prends :
Je prends z dans [x,y] (avec x dans [a1,b1] et y dans [a2,b2] et a1,a2 dans A et b1,b2 dans B) et je veux montrer que z est dans [a3,b3] avec a3 dans A et b3 dans B.
Je passe bien entendu par z = tx + (1-t)y (idem avec x pour [a1,b1] et y pour [a2,b2]).
Seulement impossible de retomber sur quelquechose du genre :
z = t'a3 + (1-t')b3...
:briques:
Quelqu'un peut-il m'aiguillonner ?
Merci d'avance.
Union de convexes, convexe ?
10 messages
- Page 1 sur 1
Salut,
pour montrer qu'un ensemble X est convexe il suffit de montrer que :
Quelques soient les points a et b dans X le segment [ab] est dans X.
Ici c'est assez facile :
Il y a 3 cas possibles
Chacun d'eux est facile à traiter.
remarque : il est clair que A et B sont inclus dans l'ensemble donné.
pour montrer qu'un ensemble X est convexe il suffit de montrer que :
Quelques soient les points a et b dans X le segment [ab] est dans X.
Ici c'est assez facile :
Il y a 3 cas possibles
- a et b sont dans A
- a et b sont dans B
- a est dans A et b est dans B
Chacun d'eux est facile à traiter.
remarque : il est clair que A et B sont inclus dans l'ensemble donné.
je vous propose ceci, avec les notations d'azboul :
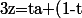b)
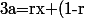y) avec
avec  et
et 
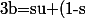v) avec
avec  et
et 
Donc:
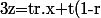.y+(1-t)s.u+(1-t)(1-s).v)
Je vais chercher.u)\in [x,u]\subset A) et
et .v)\in [y,v]\subset B) tel qu'il existe
tel qu'il existe  avec
avec 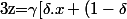.u]+(1-\gamma)[\beta.y+(1-\beta).v])
c'est à dire :
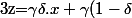.u+(1-\gamma)\beta.y+(1-\gamma)(1-\beta).v)
Soit par identification :
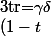s=(1-\delta)\gamma \\ t(1-r)=\beta(1-\gamma) \\ (1-t)(1-s)=(1-\gamma)(1-\beta))
Le système m'a l'air OK, on peut montrer facilement que\in[0;1]^3) , je trouve :
, je trouve :
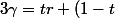s \\ \delta=\frac{tr}{tr+(1-t)s} \\ \beta=\frac{t(1-r)}{1-tr-(1-t)s})
Et on a donc bien qui appartient à un segment d'extrémités dans
qui appartient à un segment d'extrémités dans 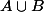 . L'union des segments joignant deux points arbitraires de A et B est donc bien convexe.
. L'union des segments joignant deux points arbitraires de A et B est donc bien convexe.
Donc:
Je vais chercher
c'est à dire :
Soit par identification :
Le système m'a l'air OK, on peut montrer facilement que
Et on a donc bien
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
