Le but est de montrer qu un espace de Banach uniformément convexe est réflexif. On prend u de E" de norme 1. Pour
Je dois montrer que pour tout f et tout epsilon, l'ensemble
Uniforme convexité => réléxivité
2 messages
- Page 1 sur 1
uniforme convexité => réléxivité
par mirlamber » 05 Déc 2012, 19:34
Bonsoir
Le but est de montrer qu un espace de Banach uniformément convexe est réflexif. On prend u de E" de norme 1. Pour
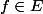
' et 
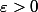
, on appelle 
l'ensemble des éléments x de E, de norme inférieur ou egale à 1 tels que  - u(f)|| <= \varepsilon)
Je dois montrer que pour tout f et tout epsilon, l'ensemble est une partie fermé et non vide de E.
Le but est de montrer qu un espace de Banach uniformément convexe est réflexif. On prend u de E" de norme 1. Pour
Je dois montrer que pour tout f et tout epsilon, l'ensemble
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :