Unicite de la forme trigonometrique d'un nombre complexe
8 messages
- Page 1 sur 1
Re: Unicite de la forme trigonometrique d'un nombre complexe
Mmmmh ... le résultat est presque vrai, mais faux tout de même.
Si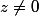 , tu ne pourras avoir l'égalité de
, tu ne pourras avoir l'égalité de  et
et  que modulo
que modulo  .
.
Et si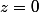 ...
...
Si
Et si
Re: Unicite de la forme trigonometrique d'un nombre complexe
Donc ton énoncé est incomplet. c'est ce que je voulais te faire remarquer.
Tu te poses des questions sur l'unicité du module d'un nombre complexe ?
Sur le fait que est le module de
est le module de ) ?
?
Peux tu rappeler la définition du module d'un nombre complexe ?
Tu te poses des questions sur l'unicité du module d'un nombre complexe ?
Sur le fait que
Peux tu rappeler la définition du module d'un nombre complexe ?
Re: Unicite de la forme trigonometrique d'un nombre complexe
Si, il y a un énoncé que tu as donné : si = r'(\cos b+i\sin b)) , alors
, alors 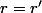 et
et  en annonçant que tu voulais le démontrer. Il est faux tel quel.
en annonçant que tu voulais le démontrer. Il est faux tel quel.
Ton énoncé est à modifier de la façon suivante : si= r'(\cos b+i\sin b),) alors
alors 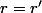 et si
et si 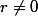 alors
alors 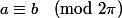 .
.
Ensuite, c'est bon pour le module ? Tu t'es convaincu que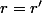 ?
?
Ton énoncé est à modifier de la façon suivante : si
Ensuite, c'est bon pour le module ? Tu t'es convaincu que
Re: Unicite de la forme trigonometrique d'un nombre complexe
Il m'a semblé pourtant m'être exprimé clairement. Bon, tant pis.
Re: Unicite de la forme trigonometrique d'un nombre complexe
salut
ben non ...
...
Et donc a = b mod (2kpi)
D'où l'unicité prouvée
ben non ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Unicite de la forme trigonometrique d'un nombre complexe
donc tu n'as pas unicité du couple (r, a) ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
