Unefonction interessante

[reginald]

bonsoir,

j'ai un probleme d maths a resoudre , ca fait quelques semaines que je cogite dessus sans pouvoir trouver toutes les reponses: f(x+y)= f(x)+f(y)/1+ f(x)f(y)
on demande de demontrer que1) f ne peut prendre ni la valeur 1 ni -1
2)f(R) inclus dans l'intervalle ouvert -1 1.
3)f(0)=0 et f est impaire.
4) si f est derivable a roite en x=0,alors elle est derivable sur
R
5)le plus important pour moi : 1+f(nx)/1-f(nx)=[1+ f(x)/1-f(x)]^n

j'ai essaye de resoudre les quatre premiers mais le dernier j'arrive pas a faire.


merci de m'apporter votre aide le plus vite que possible
:mur:

[Ericovitchi]

Ca sent furieusement la tangente hyperbolique tout ça.

Une idée pour le 5 :

Elle est vraie pour n=1,
pour n=2 tu as
Donc
et
Et donc on a bien
Tu supposes que c'est vrai pour n et tu montres que c'est encore vrai pour n+1.

[mathelot]

bonjour,

est-ce que l'on peut obtenir th() à partir de l'équation fonctionnelle ??

[Ericovitchi]

c'est ce que je me demandais aussi. En fait il faudrait trouver une équation différentielle à laquelle satisfait f(x). je n'ai pas encore cherché mais ça devrait être faisable.

[girdav]

Bonjour.
L'équation fonctionnelle est bien ?
Dans ce cas il semble que constante égale à ou à marchent.
Pour la deux utilise l'équation pour , puis .
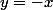
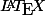
EDIT: le a des problèmes quand on met un "-" au début

[Ericovitchi]

1 OK mais pour : ca m'étonnerait.