[MPSI] Une toute petite question sur les matrices...

[pouik]

Bonjour,
Pourriez-vous me donner un exemple de matrice non nulle de ne pouvant appartenir à aucun groupe multiplicatif de ?

Merci d'avance, je ne vois absolument pas d'exemple !

[tize]

Bonsoir,
n'importe qu'elle matrice nilpotente devrait convenir...
exemple:

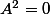
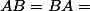
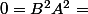
on a , ne peut donc pas appartenir à un groupe multiplicatif puisqu'alors il existerait une matrice telle que "élément neutre du groupe" et donc "élément neutre du groupe"...le groupe serait donc réduit à 0.

[cyberchand]

N'importe quelle matrice non inversible.
Si M est ds un groupe multiplicatif, alors il existe N tel que MN=I par définition du groupe...

[fahr451]

N'importe quelle matrice non inversible.
Si M est ds un groupe multiplicatif, alors il existe N tel que MN=I par définition du groupe...

faux cybermarchand

ne confonds pas groupe et sous groupe de Gl(2)

l 'étude des groupes multiplicatifs de matrices est classique

[fahr451]

on montre que pour H inclus dans Mn(K)
H est un groupe multiplicatif ssi il existe F et G supplémentaires dans K^n tels que
H = { M ; Im M = F et Ker M = G }

[yos]

L'élément neutre d'un tel groupe est diag(1,...,1,0,...,0) j'imagine.

[fahr451]

à une similitude près


en fait en travaillant avec les endomorphismes de K^n

le neutre est la projection sur F de direction G

[yos]

Un élément neutre patenté est idempotent, alors on peut permuter les 1 et les 0 sur la diagonale, mais de là à y mettre des ...

[fahr451]

je voulais dire

le neutre est E

E = P D P^(-1)

n'importe quelle matrice de projection est un neutre pour un certain groupe

pas seulement les diagonales

[yos]

ah oui il y a similitude et similitude.