Une suite définie par une integrale.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 14 Juil 2014, 10:51
par Pythales » 14 Juil 2014, 10:51
Mikihisa a écrit:Bonsoir ! Voilà je bloque sur un exo dont voici l'énoncer :
Soit f : [0;1] -> R continue telle que f(0) = 0.
Montrer que
dt = 0)
En fait je suis partie dans plein direction mais j'ai pas réussi a conclure. En passant par les définition de limite/continuité je m'y retrouve pas, ni avec des changement de variable.
J'ai proposer l'exo a une pote qui adore les maths mais n'a qu'un niveau terminale, et elle me dit "pourquoi ça marche pas de dire que t^n tend vers 0 donc f(t^n) tend vers f(0)=0 et donc le résultat ...
Ma première réponse c'est : parceque c'est trop facil xD mais en réalité je saurait même pas lui expliquer...
Déjà je prendrai avec plaisir des indices sur la résolution mais aussi pourquoi le solution de facilité ne fonctionne pas ?
Bien cordialement !
Si je pose

il vient
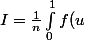u^{\frac1n-1}du)
avec
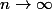
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 14 Juil 2014, 13:30
par Mikihisa » 14 Juil 2014, 13:30
Oui, j'était arriver a la aussi, mais même en faisant tendre n vers l'infini, tu obtient f(x)/x et t'es pas plus avancé. Mais le problème c'est que tu ne prouve pas que la limite existe, ni même l'intégrale (c'est d'autant plus suspect vu que x^{(1/n)-1}.f(x) n'est pas définie sur [0;1] des lors que n>2). Il me semble d'ailleurs que pour faire un changement de variable il faut que les fonctions soient "bien" i.e. Définie, continue, dérivable sur tout I, et rien ne signifie que f est dérivable sur I.
Bref tant d'indice qui pousse a penser que cette méthode n'est pas la bonne :D
Par exemple
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 14 Juil 2014, 14:58
par Mikihisa » 14 Juil 2014, 14:58
Voici comment j'ai rédiger la conclusion :
Au final on a :
Pour tout 00,
Il existe
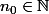
tel que pour tout
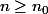
:
dt|\leq\epsilon M + (1-M).sup|f|)
Posons
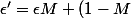.sup|f|)
, on vois que

décrit ]0;+

[ quand

et M décrivent ]0;+

[ et ]0;1[, donc on peux écrire :
dt|\leq\epsilon ')
Donc
dt)
converge et
dt = 0)
Je n'utilise pas la limite sup, ça m'a l'air pas mal en fait, le fait que eM+(1-M)suf|f| décrit ]0;+infty[ donne la définition même de la limite, en l'écrivant il ne m'a donc pas emblée nécessaire de parler de limite sup.
Merci pour ton aide encore une fois

-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 14 Juil 2014, 15:15
par Pythales » 14 Juil 2014, 15:15
Mikihisa a écrit:Bonsoir ! Voilà je bloque sur un exo dont voici l'énoncer :
Soit f : [0;1] -> R continue telle que f(0) = 0.
Montrer que
dt = 0)
En fait je suis partie dans plein direction mais j'ai pas réussi a conclure. En passant par les définition de limite/continuité je m'y retrouve pas, ni avec des changement de variable.
J'ai proposer l'exo a une pote qui adore les maths mais n'a qu'un niveau terminale, et elle me dit "pourquoi ça marche pas de dire que t^n tend vers 0 donc f(t^n) tend vers f(0)=0 et donc le résultat ...
Ma première réponse c'est : parceque c'est trop facil xD mais en réalité je saurait même pas lui expliquer...
Déjà je prendrai avec plaisir des indices sur la résolution mais aussi pourquoi le solution de facilité ne fonctionne pas ?
Bien cordialement !
Une autre méthode ?
Ecrire que

On peut déterminer

pour minimiser la 2ème intégrale.
Pour la 1ère, écrire :

car

d'où la conclusion
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
dt = 0)
