Une Spirale

[v3x0]

Bonjour a tous! je m'entraine pour des examen, et je tombe sur un exercice a propos des suite:
On considère la suite Un de nombre complexes tels que pour tout n appartenant a N on ait:
(Un+2)= 2i*(Un+1 )+( Un)
Mn, le point du plan d'affixe Un

On me demande:
1) Soit n appartenant à N. Comment peut on construire Mn+2 en fonction de Mn+1 et Mn?
2 On suppose de plus que u0=u1=1
a) Calculer u2, u3, u4, u5 en représenter M1.....M5
b) Pour tout n appartenant, exprimer Un en fonction de n





1) On a Mn+2 affixe Un+2
soit (Mn+2) affixe 2i*(Un+1)+(Un)
Donc (Mn+2)= 2i*(Mn+1)+(Mn)
(Pas très sur)


2) a) u2=2i+1; u3=2i-3; u4=-4i-3; u5=-4i+5

b) ???

Voila, je ne sais pas du tout comment faire la question b)...

Est-ce que quelqu'un pourrait m'éclairer svp? Merci d'avance!

[aymanemaysae]

Pour la question n° 1, pour construire un point 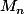il faut construire son affixe z ( ici) qui est un nombre complexe sous la forme x + i y , qui permet de construire le point M_n(x,y) .

Vous avez écrit:

1) On a Mn+2 affixe Un+2
soit (Mn+2) affixe 2i*(Un+1)+(Un)
Donc (Mn+2)= 2i*(Mn+1)+(Mn)
(Pas très sur)

Ceci contient quelques erreurs, que j'essaierai de réctifier :

1) On a le point Mn+2 d'affixe Un+2, donc le point (Mn+2) a pour affixe 2i*(Un+1)+(Un).
avec ce résultat vous pouvez construire le point M_n+2 :
M_n+2(partie réelle de U_n+2, partie imaginaire de U_n+2) .

Quant à dire : donc (Mn+2)= 2i*(Mn+1)+(Mn) , c'est à éviter.

Pour la question n° 2-a , vos calculs sont justes.

Pour la question 2-b, est - ce que vous avez étudié les suites récurrentes?

[zygomatique]

salut

tu fais l'effort d'utiliser des parenthèses et c'est bien .... mais il serait mieux de les placer au bon endroit !!!

u(n + 2) = 2iu(n + 1) + u(n)


faire la question 2/ peut permettre de répondre à la question 1/

... sinon remarquer que u(n + 2) - iu(n + 1) = i[u(n + 1) - iu(n)]