Une série : moyenne de Cesàro
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 03 Aoû 2014, 16:45
par Mikihisa » 03 Aoû 2014, 16:45
Soit
_{n\in\mathbb{N}^*})
une suite réelle, j'ai la suite suivante :

Je cherche a montrer que si
)
tend vers

alors
)
aussi.
Je vois que si (un) converge vers l, elle est bornée et alors (vn) aussi est bornée.
De plus si j'ai

Et chaque terme de la somme a la fin est inférieur a

Et donc la somme a la fin est inférieur a

Mais je n'arrive pas a conclure, au mieux on arrive a majorer par

mais ça ne suffit pas :/. Suis-je partie dans la mauvais direction ?
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 03 Aoû 2014, 17:05
par jlb » 03 Aoû 2014, 17:05
tu n'aurais pas confondu N et n pour majorer ce qui te gène?
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 03 Aoû 2014, 17:32
par Mikihisa » 03 Aoû 2014, 17:32
Heuuu je crois pas :hein:
J'ai raisonner comme suis : déjà si (un) est bornée (vn) est bornée aussi (rapide calcul d'inégalité).
En fait si n>N j'ai

avec
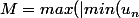,|max(u_n)|))
Et ça me permet pas de conclure

donc j'ai du me tromper dans mon raisonnement.
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 03 Aoû 2014, 17:47
par jlb » 03 Aoû 2014, 17:47
J'ai raisonner comme suis : déjà si (un) est bornée (vn) est bornée aussi (rapide calcul d'inégalité).
n fait si n>N j'ai
 Là, IL Y A UN PB ENTRE N et n
Là, IL Y A UN PB ENTRE N et n 
avec
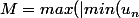,|max(u_n)|))
oui, tu as confondu le n et le N!! pour conclure, après avoir découpé ta somme, tu majores les |u_i -l| pour i=1 à N mais tu as la liberté de prendre ton n>N aussi grand que tu veux: c'est cela qui va permettre de dégager ce qui te gène!!
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 03 Aoû 2014, 17:56
par Mikihisa » 03 Aoû 2014, 17:56
En fait non , enfin si j'ai fait une coquille, en effet ce n'est v_N mais

ce qui effectivement n'est pas du tout la même chose ^^
Mais j'ai penser a ça, le fait que je puis prendre n aussi grand que je veux... (J'viens de trouver je crois) je dis que 1/n*somme... (La somme qui ne dépend du coup plus de n, donc est "constante" tend vers 0 donc je peux la majorer par epsilon mmmhh c'est ça ?
(D'ailleurs dans mon premier message je n'ai pas écrit v_N ^^)
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 03 Aoû 2014, 18:24
par Mikihisa » 03 Aoû 2014, 18:24
Bon j'ai une preuve en tête je la rédige et je la poste tu le dira si j'ai fait des coquille ( si tu veux bien )
Merci ^^
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 03 Aoû 2014, 18:24
par jlb » 03 Aoû 2014, 18:24
Mikihisa a écrit:En fait non , enfin si j'ai fait une coquille, en effet ce n'est v_N mais

ce qui effectivement n'est pas du tout la même chose ^^
Mais j'ai penser a ça, le fait que je puis prendre n aussi grand que je veux... (J'viens de trouver je crois) je dis que 1/n*somme... (La somme qui ne dépend du coup plus de n, donc est "constante" tend vers 0 donc je peux la majorer par epsilon mmmhh c'est ça ?
(D'ailleurs dans mon premier message je n'ai pas écrit v_N ^^)
oui, cela a l'air de tenir pour l appartenant à R!!!! :bad: tu as encore à mettre en place la démo pour l=+/-inf! bon courage :ptdr:
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 03 Aoû 2014, 19:34
par Mikihisa » 03 Aoû 2014, 19:34
Ouais en fait j'ai dit que
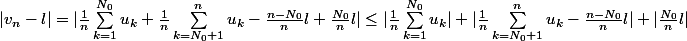
Ensuite je majore le terme du milieu par

en transformer un peu pour avoir la (1/n)somme des |uk-l|, je dit que les deux autre membre converge vers 0 donc je peux trouver N_1 et N_2 où pour tout n>N_1 le premier terme est N=max(N0,N1,N2)
La je bloque sur une autre question ^^ je doit montrer que si (un) est monotone et si (vn) converge (un) converge, mais je vais chercher un peu ^^
Le reste du TD ça a l'aire d'aller sauf 2exo intituler "critère de concentration" et "critère de Razbe-Duhamel"
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 03 Aoû 2014, 21:20
par Mikihisa » 03 Aoû 2014, 21:20
Omg c'était ridiculement simple .......
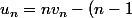v_{n-1}/)
et j'ai galerer pendant 1h pour trouver ça vite fait au moment ou j'allais abandonné....
-
Ingrid55
- Membre Relatif
- Messages: 162
- Enregistré le: 06 Juil 2014, 21:51
-
 par Ingrid55 » 03 Aoû 2014, 21:31
par Ingrid55 » 03 Aoû 2014, 21:31
Il faudrait penser au théorème des gendarmes ...
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 03 Aoû 2014, 21:42
par Mikihisa » 03 Aoû 2014, 21:42
Pour quelle question ?
-
Ingrid55
- Membre Relatif
- Messages: 162
- Enregistré le: 06 Juil 2014, 21:51
-
 par Ingrid55 » 03 Aoû 2014, 21:48
par Ingrid55 » 03 Aoû 2014, 21:48
J'ai rien dit ^^ , continues dans ta lancée ...
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 03 Aoû 2014, 21:50
par jlb » 03 Aoû 2014, 21:50
Mikihisa a écrit:Omg c'était ridiculement simple .......
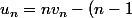v_{n-1}/)
et j'ai galerer pendant 1h pour trouver ça vite fait au moment ou j'allais abandonné....
Et alors, tu peux développer???
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 03 Aoû 2014, 21:55
par Mikihisa » 03 Aoû 2014, 21:55
Bah vn est bornée, m2 (ou égal) on a
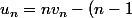v_{n-1})
donc
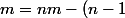m<u_n<nM-(n-1)M=M)
Donc un est minoré par min(u1,m) et majore par max(u1,M), si elle est monotone en plus elle converge.
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 03 Aoû 2014, 21:57
par jlb » 03 Aoû 2014, 21:57
Mikihisa a écrit:Bah vn est bornée, m2 (ou égal) on a
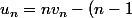v_{n-1})
donc
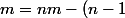m<u_n<nM-(n-1)M=M)
Donc un est minoré par min(u1,m) et majore par max(u1,M), si elle est monotone en plus elle converge.
les encadrements cela ne fonctionnent pas trop comme cela!!!
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 03 Aoû 2014, 22:05
par Mikihisa » 03 Aoû 2014, 22:05
Mmmh c'est le - qui pose problème c'est ça ? Jsuis fatigue moi ...
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 03 Aoû 2014, 22:10
par jlb » 03 Aoû 2014, 22:10
Mikihisa a écrit:Mmmh c'est le - qui pose problème c'est ça ? Jsuis fatigue moi ...
Oui!!, je te propose une autre piste: la suite u est monotone (par exemple croissante)qu'en déduis-tu?
Et du coup, que te dit le théorème de Césaro?
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 03 Aoû 2014, 22:19
par Mikihisa » 03 Aoû 2014, 22:19
Le théorème de cesaro c'est la question d'avant c'est ça ? (En passant yavais la demo sur Wikipedia loool, mais content de l'avoir fait par moi même quand même)
J'en déduis pas grand chose, un+1>un, (un) est minoré... Toussa ça me dit pas que un a une limite :/
Ah tu voulais dire que je déduise que si un est monotone, vn l'est aussi c'est ça ?
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 03 Aoû 2014, 22:27
par jlb » 03 Aoû 2014, 22:27
Mikihisa a écrit:Le théorème de cesaro c'est la question d'avant c'est ça ? (En passant yavais la demo sur Wikipedia loool, mais content de l'avoir fait par moi même quand même)
J'en déduis pas grand chose, un+1>un, (un) est minoré... Toussa ça me dit pas que un a une limite :/
Ah tu voulais dire que je déduise que si un est monotone, vn l'est aussi c'est ça ?
si u est croissante, il peut lui arriver quoi? réfléchis à cela et après, tu reliras ce que te dis le théorème que tu as presque démontré ( cas l=+/-infini???) et tu auras ta réponse ( euh ou pas :we: )
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 03 Aoû 2014, 22:32
par Mikihisa » 03 Aoû 2014, 22:32
Lol, soit elle tends vers l'infini et la moyenne tend aussi vers l'infini, soit elle converge c'est ça ? Comme la moyenne converge on est dans le premier cas.
Un raisonnement par l'absurde un peu alambiqué. En fait tu veux dire que un a forcément une limite (infini ou pas) car elle est monotone c'est ça ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
