Une série entiére comme polynome?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
NICO 97
- Membre Relatif
- Messages: 137
- Enregistré le: 24 Mar 2008, 20:33
-
par NICO 97 » 20 Aoû 2008, 18:26
Bonjour,
Je ne comprend pas la correction d'un exercice.
Il s'agit de trouver 2 polynômes U et V qui vérifient:
r>=1 s>=0
deg(U)<r
^{s + 1} U + x^r V = 1\])
On donne comme solution:
} x^q <br />\])
et
^{s + 1} \sum\limits_{q = r}^\infty {\left( {\begin{array}{{}}<br /> {s + q} \\<br /> s \\<br /><br /> \end{array} } \right)} x^{q - r} <br />\])
Ce qui me choque c'est que, pour moi, V n'est pas un polynôme puisque les coefficients vont à l'infinie. Un polynôme est bien défini comme étant à support fini.
Sinon, tout ceci découle du fait que l'on a montré que:
^{s + 1} }} = \sum\limits_{q = 0}^\infty {\left( {\begin{array}{{}} {s + q} \\ s \\\end{array}} \right)} x^q \])
Merci d'avance.
PS, je ne comprend pas non plus pourquoi il y a un dollar dans mes formules.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
par Doraki » 20 Aoû 2008, 19:02
V est bien un polynôme, c'est juste que en multipliant la série infinie par (1-x)^(s+1), tu vas voir qu'au bout d'un moment, tous les coefficients de V seront égaux à 0.
Utilise ta dernière équation pour réécrire V.
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
par magnolia86 » 20 Aoû 2008, 19:20
NICO 97 a écrit:Il s'agit de trouver 2 polynômes U et V qui vérifient:
r>=1 s>=0
deg(U)<r
Passer par les fractions rationnelles et les séries pour un truc nettement moins compliqué, c'est un peu étrange...
On écrit
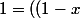+x)^{r+s} \in \sum_{i=0}^{r+s} C_{r+s}^i.(1-x)^i.x^{r+s-i})
(
binome de Newton)
On trie alors les termes de la somme :
-- pour
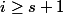
le terme est multiple de
^{s+1})
, et
-- pour
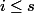
le terme est multiple de
.
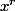
En regroupant les termes ainsi, on obtient
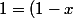^{s+1}.U + x^r.V)
avec
^i.x^{s-i})
^{i-s-1}.x^{r+s-i}<br />=\sum_{i=1}^{r} C_{r+s}^{i+s}.(1-x)^{i-1}.x^{r-i})
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
par magnolia86 » 20 Aoû 2008, 19:47
NICO 97 a écrit:Bonjour,
Je ne comprend pas la correction d'un exercice.
Il s'agit de trouver 2 polynômes U et V qui vérifient:
r>=1 s>=0
deg(U)<r
On donne comme solution:
et
Ce qui me choque c'est que(...)
Moi, ce qui me choque, c'est que V s'annule quand x=1, donc
^{s + 1} U + x^r V = 1)
n'est pas vrai...
-
NICO 97
- Membre Relatif
- Messages: 137
- Enregistré le: 24 Mar 2008, 20:33
-
par NICO 97 » 20 Aoû 2008, 19:52
magnolia86 a écrit:Moi, ce qui me choque, c'est que V s'annule quand x=1, donc
n'est pas vrai...
En fait on a dit que c'était vrai sur ]-1,1[
-
NICO 97
- Membre Relatif
- Messages: 137
- Enregistré le: 24 Mar 2008, 20:33
-
par NICO 97 » 20 Aoû 2008, 19:54
Doraki a écrit:V est bien un polynôme, c'est juste que en multipliant la série infinie par (1-x)^(s+1), tu vas voir qu'au bout d'un moment, tous les coefficients de V seront égaux à 0.
Utilise ta dernière équation pour réécrire V.
Je vois pas comment démarrer.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
par Doraki » 20 Aoû 2008, 20:05
J'appelle
 x^q})
Grâce au résultat que tu as montré,
^{s+1} S = 1)
La différence entre la série que tu as dans V et S, c'est juste un polynôme (un vrai, de degré fini) donc tu peux exprimer V seulement avec S et des polynômes. Comme dans V, la série est multipliée par (1-x)^(s+1), tu vas pouvoir éliminer S avec cette égalité.
-
magnolia86
- Membre Relatif
- Messages: 155
- Enregistré le: 14 Aoû 2008, 17:59
-
par magnolia86 » 20 Aoû 2008, 20:30
NICO 97 a écrit:En fait on a dit que c'était vrai sur ]-1,1[
Je suis bête... tellement absorbé par les polynômes, j'en avais oublié le rayon de convergence de la série. :bad:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
