Une question sur (Z/nZ)* please
29 messages
- Page 2 sur 2 - 1, 2
Disons plutôt le contraire
Au commencement sont les groupes, et l'ordre d'un groupe fini est son nombre d'éléments.
Ensuite sont les éléments de ce groupe. Chacun d'eux engendre un cycle, qui est un sous-groupe (commutatif) du groupe en question, et l'ordre de ce sous-groupe est aussi l'ordre de l'élément. Ces deux notions sont effectivement très proches.
Attention toutefois, l'ordre d'un groupe n'est pas lié de façon simple à l'ordre de ses éléments, par exemple dans^n) , tous les éléments sont d'ordre 2 (sauf le neutre).
, tous les éléments sont d'ordre 2 (sauf le neutre).
Au commencement sont les groupes, et l'ordre d'un groupe fini est son nombre d'éléments.
Ensuite sont les éléments de ce groupe. Chacun d'eux engendre un cycle, qui est un sous-groupe (commutatif) du groupe en question, et l'ordre de ce sous-groupe est aussi l'ordre de l'élément. Ces deux notions sont effectivement très proches.
Attention toutefois, l'ordre d'un groupe n'est pas lié de façon simple à l'ordre de ses éléments, par exemple dans
J'accepte tout à fait que les choses soient ainsi, je déplore seulement qu'un même terme soit employé pour deux choses différentes, d'autant plus que ces choses sont proches et utilisées dans un même contexte, car la confusion est alors plus facile. Et puisque pour le nombre d'éléments d'un groupe fini, il existe déjà le terme cardinal (qui est d'ailleurs plus général, puisqu'il s'applique à tout ensemble), je préfère, tant que j'en ai la possibilité, utiliser ce dernier terme.
:happy3:
:happy3:
En fait pour définir l'ordre d'un élement passe par le fait que ce soit l'ordre du groupe engendré par cet élément, et là ca va bien, et ca évite d'utiliser deux mots pour la même chose après.
Dans les deux cas on aurait un blocage, soit on utilise deux mots pour la même idée, soit on utilise le même mot pour quelque chose de proche mais de différent malgré tout.
A+
Dans les deux cas on aurait un blocage, soit on utilise deux mots pour la même idée, soit on utilise le même mot pour quelque chose de proche mais de différent malgré tout.
A+
Salut, quinto : dans le 1er cas, on n'a pas de blocage :
Si pour désigner tout cardinal, on n'employait que le terme cardinal, alors dans le cas d'un groupe engendré par un élément, on n'aurait qu'à dire : le cardinal du groupe engendré par un élément est égal à l'ordre de cet élément (en définissant l'ordre comme le plus petit entier str. positif...).
Mais les choses ne sont pas ainsi, et il me faut les accepter telles qu'elles sont. :briques:
:happy3:
Si pour désigner tout cardinal, on n'employait que le terme cardinal, alors dans le cas d'un groupe engendré par un élément, on n'aurait qu'à dire : le cardinal du groupe engendré par un élément est égal à l'ordre de cet élément (en définissant l'ordre comme le plus petit entier str. positif...).
Mais les choses ne sont pas ainsi, et il me faut les accepter telles qu'elles sont. :briques:
:happy3:
Je vois que la discussion s'est emballée au dela de (Z/nZ)*; Tant mieux d'ailleurs c'est signe de vivacité et de fecondité dans le forum.
Sans avoir lu toutes les contrib, je donne mon avis qui me parait assez clair (je l'ai assez etudié) et coherent sur cette notion.
-Ordre d'un groupe fini ou non := cardinal de ce groupe (qui vaut donc eventuellement l'infini).
-Ordre d'un element x G := le plus petit entier n > 0 (s'il existe) tel que x^n = e (element neutre du groupe)
-Pont entre ces deux definitions qui utilisent le meme mot ( ordre): c'est que par hasard (et meme heureusement) le cardinal du sous groupe engendré par x:=, est aussi egal a l'ordre de l'element x.
-D'ou, pour un groupe cyclique , ou cette notion d'ordre pourrait avoir un double sens, il se trouve que l'ordre de a c'est pile poil le cardinal de .
Dans ce cas, les deux definitions s'equivalent: ord(a) = + ptit n>0 tq a^n = 0 et c'est aussi card().
Je pense que les choses restent coherentes!
RadarX.
Sans avoir lu toutes les contrib, je donne mon avis qui me parait assez clair (je l'ai assez etudié) et coherent sur cette notion.
-Ordre d'un groupe fini ou non := cardinal de ce groupe (qui vaut donc eventuellement l'infini).
-Ordre d'un element x G := le plus petit entier n > 0 (s'il existe) tel que x^n = e (element neutre du groupe)
-Pont entre ces deux definitions qui utilisent le meme mot ( ordre): c'est que par hasard (et meme heureusement) le cardinal du sous groupe engendré par x:=
-D'ou, pour un groupe cyclique , ou cette notion d'ordre pourrait avoir un double sens, il se trouve que l'ordre de a c'est pile poil le cardinal de .
Dans ce cas, les deux definitions s'equivalent: ord(a) = + ptit n>0 tq a^n = 0 et c'est aussi card().
Je pense que les choses restent coherentes!
RadarX.
Le groupe multiplicatif de l'anneau 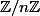 est cyclique si et seulement si l'entier
est cyclique si et seulement si l'entier 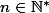 a l'une des formes suivantes :
a l'une des formes suivantes :  ,
, 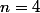 ,
, 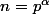 ,
, 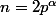 (avec
(avec  premier impair et
premier impair et 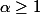 ). Ce n'est pas trivial à démontrer.
). Ce n'est pas trivial à démontrer.
On montre par contre assez facilement que tout sous-groupe fini du groupe multiplicatif d'un corps (commutatif, sinon ça ne marche pas) est cyclique. Peut-être une confusion avec ce dernier résultat est-elle à l'origine de la discussion ?
On montre par contre assez facilement que tout sous-groupe fini du groupe multiplicatif d'un corps (commutatif, sinon ça ne marche pas) est cyclique. Peut-être une confusion avec ce dernier résultat est-elle à l'origine de la discussion ?
Alpha a écrit:Pour RadarX,
...ce n'est pas que si (Z/nZ)* est cyclique, un élément de (Z/nZ)* ne peut pas être son propre symétrique, mais que si (Z/nZ)* est cyclique, on ne peut pas trouver 2 éléments distincts de (Z/nZ)* qui soient chacun leur propre inverse.
Distincts et non neutres, veut dire Alpha?
Et est ce vrai dans n'importe quel groupe cyclique ca? IE que si G cyclique alors on ne peut voir 3 elements distincts (1, x et y) qui sont leurs propres symetriques?
29 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
