Cordialement.
Une propriété d'Algère général, trop jolie.
18 messages
- Page 1 sur 1
Re: une propriété d'Algère général, trop jolie.
Si on note w une racine de  (qui n'a pas de racine double) on a :
(qui n'a pas de racine double) on a :
^2} =( w^{2n+1})^{2n+1} (w^{2n+1})^{-2k} w^{k^2} = (-1) \times 1 \times w^{k^2}=-w^{k^2})
En écrivant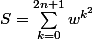 , on obtient
, on obtient 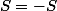 (via le changement d'indice k <- 2n+1-k).
(via le changement d'indice k <- 2n+1-k).
Donc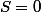 ce qui permet de conclure le résultat.
ce qui permet de conclure le résultat.
En écrivant
Donc
Re: une propriété d'Algère général, trop jolie.
oui, bravo.
J'aimerais savoir, si d'autres diviseurs sont connues, manière de pouvoir avoir une forumule clause pour cette somme.
J'aimerais savoir, si d'autres diviseurs sont connues, manière de pouvoir avoir une forumule clause pour cette somme.
Re: une propriété d'Algère général, trop jolie.
Pour la formule clause de la somme il me semble avoir trouvé une formule plutôt intéressante mais il reste du travail à effectuer dessus et je ne suis pas sûr qu'on puisse arriver au bout :
\right)^{ln(a) })
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
Re: une propriété d'Algère général, trop jolie.
Ta formule (si elle est juste) est aussi longue que celle de départ, donc cela semble avoir un intêret restreint.
Re: une propriété d'Algère général, trop jolie.
note bien que au départ il y a un carré dans la puissance ce qui pose problème (sinon on aurait pu simplement utiliser la formule de pour les termes successifs d'une suite géométrique) alors que à la fin il n'y en a plus de plus j'imagine qu'il existe des formules pour évaluer les sommes de fonctions Gamma donc on ne doit plus être trés loin du résultat malheureusement j'ai bac dans 2h du coup je ne peux pas chercher plus longtemps mais libre à toi de continuer de ton côté ^^
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
Re: une propriété d'Algère général, trop jolie.
Viko a écrit:j'imagine qu'il existe des formules pour évaluer les sommes de fonctions Gamma donc on ne doit plus être trés loin du résultat
Euh.. Tu trouves que sommer des puissances entières (carrés) de a compliqué mais une somme de fonction gamma puissance ln(a) plus facile ? :p
Saurais-tu déjà calculer Gamma(1/2) ? Pas super facile !
En revanche exprimer les Gamma(k+1/2) en fonction des Gamma(k+1/2) d'avant est faisable par une IPP
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: une propriété d'Algère général, trop jolie.
Oui, Gamma(1/2) = racine de pi il me semble. J'avais fait la démonstration ya qlq mois mais je t'avoue ne pas m'en souvenir exactement je crois qu'il faut passer par une gaussienne mais je ne suis plus sûr enfin bref..Je suis d'accord que passer d'une bête somme d'entier à une somme de fonction de gamma peut paraître pas très judicieux mais j'ai l'intuition (rien de très mathématiques..) que sa peut fonctionner car comme tu l'a dit Gamma(k+1/2) et Gamma(k) sont intimement liés et comme k est un entier je pense qu'après un simple passage de Gamma(k) à (k-1)! on devrait pouvoir s'en sortir sans trop de problème mais comme je l'ai dit le bac d'anglais m'attends donc je n'ai pas trop le temps de faire sa maintenant ^^
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
Re: une propriété d'Algère général, trop jolie.
@Viko : a-t-on =X^{\text{pgcd}(2n+1,2m+1) }+1) ?
?
Si, oui, pourquoi ?
Si, oui, pourquoi ?
Modifié en dernier par Arbre le 20 Juin 2017, 16:12, modifié 2 fois.
Re: une propriété d'Algère général, trop jolie.
Oui j'ai lu un papier qui parlait ce truc c'est bien vrai, par contre il va falloir me donner un peu de temps pour que je réfléchisse à une démonstration digne de ce nom avec une "double récurrence" (on montre que l'égalité est vrai pour n = 0 et pour tout m puis aprés on fait une récurrence classique sur n) sa marcherait non ?
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
Re: une propriété d'Algère général, trop jolie.
Possible, mais mon explication n'utilise pas cette méthode (double récurrence)
Re: une propriété d'Algère général, trop jolie.
Oui aprés la "double récjrrence c'est une méthode un peu bourrine il doit y avoir plus efficace et bien plus élégant, je serais curieux de voir la démonstration que tu as fait de ton côté ^^
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
Re: une propriété d'Algère général, trop jolie.
merci 
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
Re: une propriété d'Algère général, trop jolie.
@arbre il y'a un pbl avec ton égalité je viens de trouver une infinité d'entier qui ne la vérifie pas !
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
Re: une propriété d'Algère général, trop jolie.
Donne 2 exemples, merci.
PS : j'ai modifié mon résultat, il y avait une coquille.
PS : j'ai modifié mon résultat, il y avait une coquille.
Re: une propriété d'Algère général, trop jolie.
pour m = n = 1 et X = 5 par exmple on a : 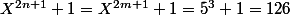
de plus=pgcd(1;1)=1) donc
donc}+1=5^{2 \times 1}+1 = 26)
et je ne te fais pas l'affront de t'expliquer pourquoi\neq 26)
plus géneralement \in \mathbb{N}^3) tel que n = m l'égalité :
tel que n = m l'égalité : =X^{2pgcd(n;m)}+1)
n'est pas vérifié !
EDIT : oui maintenant que tu l'a modifié sa marche en effet (enfin je crois)
de plus
et je ne te fais pas l'affront de t'expliquer pourquoi
plus géneralement
n'est pas vérifié !
EDIT : oui maintenant que tu l'a modifié sa marche en effet (enfin je crois)
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
Re: une propriété d'Algère général, trop jolie.
on suppose m < n et on note d le pgcd de m et n puis on pose m = du, n = dv avec pgcd (u, v) = 1 et enfin w = v - u
si P divise les polynomes et
et  alors il divise leur différence
alors il divise leur différence
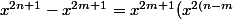} - 1) = x^{2m + 1}(x^{dw} - 1)(x^{dw} + 1))
évidemment P ne contient pas de puissance de x donc P divise(x^{dw} + 1))
or la différence de ces deux facteurs est 2 donc ces deux facteurs sont premiers entre eux
donc P divise ou divise
ou divise 
....
si P divise les polynomes
évidemment P ne contient pas de puissance de x donc P divise
or la différence de ces deux facteurs est 2 donc ces deux facteurs sont premiers entre eux
donc P divise
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
