Une petite question sur l'intégration

[pouik]

Bonjour,
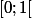
Je dois calculer une primitive de sur , puis sur .
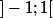
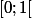
Donc je l'ai calculé sur et ensuite j'ai remarqué que la fonction ci-dessu était impaire, donc :
avec
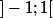
Mais puis-je me servir de ceci pour déterminer une primitive de sur ? et si oui comment ?

Merci d'avance pour vos réponses. :id: :happy2:

[fahr451]

bonjour

si oui on saurait calculer une primitive de toute fonction continue impaire...

[mathelot]

Bonjour,
ça ne répond sans doute pas à ta question, mais si f est continue et impaire,
est paire.

Sinon, toute fonction est la somme de façon unique d'une fonction paire et d'une fonction impaire:

[pouik]

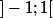
mais donc en fait pour calculer l'intégrale sur , on doit tout refaire ? ou peut-on utiliser ce que j'ai dit : en prenant , et comme ca l'intégrale est nulle.

[mathelot]

Il me semble que tu confonde intégrale et primitive.
L'intégration est plus général que le primitivation.
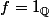
Par exemple, si est l'indicatrice des rationnels,
, ce qui montre que f n'admet pas de primitive.

[pouik]

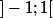
donc je doit tout refiare sur : il n'y a pas d'échapatoire ? :briques:

[mathelot]

Si tu parles de l'intégrale , elle est nulle de -1 à 1.
Pour l'intégrale:

elle s'évalue avec la primitive F de f qui s'annule en zéro et qui est paire:

[pouik]

Mais le , est-ce que ca correspond à la primitive de que j'ai calculé sur [ ?

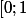
Si tu parles de l'intégrale , elle est nulle de -1 à 1.
Pour l'intégrale:

elle s'évalue avec la primitive F de f qui s'annule en zéro et qui est paire:

De plus, ce n'est pas un peu bizarre de calculer alors que n'est pas définie en ? :hum: :hum:

[mathelot]

non, tout est ok. voir mon post précédent.
C'est une intégrale généralisée. La fonction à intégrer est infinie mais sa primitive
est continue en

[pouik]

donc après avoir calculé l'intégrale sur [0;1[, je peux directement mettre votre avant dernier message sans plus de justifications ?!

PS : Pourquoi parlez vous d'intégrale généralisée, je n'en vois pas ici. :cry: :cry:

[mathelot]

donc après avoir calculé l'intégrale sur [0;1[, je peux directement mettre votre avant dernier message sans plus de justifications ?!

oui.

PS : Pourquoi parlez vous d'intégrale généralisée, je n'en vois pas ici.

Parce que la fonction que l'on intégre n'est pas définie aux bornes de l'intervalle.
Du point de vue de l'intégrale de Riemann, c'est une intégrale généralisée.
Pour Lebesgue, c''est une intégrale classique.