Une petite démo avec les complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
math*
- Membre Rationnel
- Messages: 544
- Enregistré le: 04 Déc 2006, 17:05
-
 par math* » 15 Sep 2007, 20:03
par math* » 15 Sep 2007, 20:03
bonsoir comment feriez vous pour démontrer ceci:

-
mathelot
 par mathelot » 15 Sep 2007, 20:28
par mathelot » 15 Sep 2007, 20:28
Bonjour,
on élève au carré.
on utilise les identités:
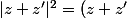(\bar{z}+\bar{z'}))
et

au final, après simplification, on trouve que l'inégalité initiale équivaut à:
}^2 \geq 0)
cordialement,
-
math*
- Membre Rationnel
- Messages: 544
- Enregistré le: 04 Déc 2006, 17:05
-
 par math* » 15 Sep 2007, 20:58
par math* » 15 Sep 2007, 20:58
bonjour mathelot. cest en effet ce que j'avais fait mais je n'avais pas vu le carré a la fin! par contre tu nas pas oublier un bout du développement dans le 2eme membre? a la fin jarrive a :
^2+2|z_1^2-z_2^2|>=0)
. êvidement le résultat est le meme!
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 15 Sep 2007, 21:42
par fahr451 » 15 Sep 2007, 21:42
bonsoir
c'est bien évidemment une conséquence de l inégalité triangulaire
appliquée à
z1 = (z1+z2)/2 + (z1-z2)/2
et à
z2 = (z1+z2)/2 - (z1-z2)/2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
