Une limite nulle

[AceVentura]

Bonsoir !
Alors je vous le remet, vu que c'est une question différente (même si dans le même "genre"). On dit que f vérifie la condition (*) si :
est de classe et , , .
On pose et il faut prouver que la limite de est nulle lorsque x tend vers 0.

Donc mon idée c'était Taylor-Young :

Donc comme :

Et donc :
qui tend vers 0 lorsque x tend vers 0.

Autre question que je n'arrive pas à faire :
Montrer que si , ou bien f est une fonction polynôme ou bien au voisinage de .

Merci de vos aides !

[alavacommejetepousse]

bonjour

si f est un polynôme rien à faire

sinon pour n fixé f^(n+1) n'est pas nulle donc on choisit a où elle ne s'annule pas on écrit FT RI entre a et x à l'ordre n+1 on minore le reste par 0 et on a que f(x) est minoré par un polynôme de degré n+1 d'où le résultat.

[AceVentura]

Je ne saisi pas trop votre indication. FT RI ?! C'est quoi :hein:

Par ailleurs, il faut que je précise le contexte je pense.
On a montré que si une fonction vérifie (*), alors elle est développable en série entière au voisinage de 0. (FAIT)

On a également montré que f vérifie (*) et s'annule en un point, alors c'est la fonction nulle. (FAIT)

Enfin on a montré que les fonctions vérifiant (*) et telle qu'il existe p avec possédant un zéro, alors f est polynômiale de degré au plus p-1. (FAIT)

Viens ensuite cette question...
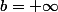
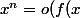Montrer que si , ou bien f est une fonction polynôme ou bien au voisinage de .

[Ben314]

Salut,
"FT", à froid, je vois pas trop, mais, vu le contexte, je pense que "RI"=avec reste intégral.
Je te laisse deviner qui est "FT"...

[MacManus]

bjr.
FT RI je pense qu'il voulait dire Formule de Taylor avec Reste Intégral...

[AceVentura]

Ok !
Mais est-ce si évident que ça lorsque f est un polynôme ?
:hein:

[Ben314]

Vu la question, ça n'as pas à "être évident" ou "ne pas être évident".
On te demande de montrer que :
"Si ???(1) alors f est un polynôme ou bien ???(2)"
Donc pour faire la preuve, tu considère une fonction f qui vérifie ???(1) et qui n'est pas un polynôme et tu doit montrer qu'elle vérifie forcément ???(2)

[AceVentura]

Ok. On sait que :
f est polynomiale.
Par contraposition, f n'est pas polynomiale .

On se donne donc un entier avec ne s'annulant pas sur , c'est-à-dire qu'il existe avec (on retombe sur les indications de "alavacommejetepousse")

C'est bien ça ?

[Ben314]

Il me semble bien que oui.

[AceVentura]

Soit donc avec ne s'annulant pas sur .
Donc il existe avec

Alors, en écrivant FTRI à l'ordre entre et je trouve que :


Donc en divisant par x^n, je trouve :


Et la dernière quantité tend vers l'infini, car n'est pas nul.

Ainsi et donc . Ce qui est .

[AceVentura]

Me trompe-je ?!

[AceVentura]

1) Soit ; montrer que .

2) Si , montrer que ou bien f est une fonction polynôme ou bien au voisinage de .
------
Preuve :

1) On a donc
et qui tend vers 0 lorsque x tend vers 0.

2) Soit tel que ne s'annulant pas sur . Il existe alors tel que . On écrit FTRI à l'ordre entre et :


En divisant par :
et qui tend vers l'infini car n'est pas nul.

Donc et donc . Ce qui est .


J''espère que c'est correct
Quelqu'un peut-il me confirmer/infirmer ?
Merci !