Une limite avec une fonction injective.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Agouraptor
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Oct 2018, 19:54
-
 par Agouraptor » 27 Déc 2020, 21:01
par Agouraptor » 27 Déc 2020, 21:01
Bonjour. Je bloque depuis quelques jours sur un problème. Si quelqu'un aurait juste une piste de départ que je pourrais creuser, ce serait sympa

. Merci en avance de vos réponses.
Exercice :
Soit

une fonction injective. Montrer que :
}{k^2} = + \infty)
-
mathelot
 par mathelot » 28 Déc 2020, 00:03
par mathelot » 28 Déc 2020, 00:03
bonsoir,
Agouraptor a écrit:Bonjour. Je bloque depuis quelques jours sur un problème. Si quelqu'un
avait juste une piste de départ que je
puisse creuser, ce serait sympa

. Merci en avance de vos réponses.
Après Si , on ne met pas le conditionnel
l'idée est de minorer cette série par une série en 1/n (on sait que la série harmonique diverge vers

)
on sait que
 Lemme: comment minorer la somme f(1)+f(2)+...+f(k)
Lemme: comment minorer la somme f(1)+f(2)+...+f(k) ?
sommation d'Abel:la sommation d'Abel est utilisée pour l'étude des séries alternées. on va l'utiliser ici:
on pose
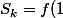+f(2)+...+f(k))
pour k entier naturel strictement positif
réécrire la série
}{k^2})
avec l'aide de la sommation d'Abel.
https://fr.wikipedia.org/wiki/Sommation_par_partiesen déduire une minoration de la série.
en déduire qu'elle diverge.
-
mathelot
 par mathelot » 28 Déc 2020, 13:51
par mathelot » 28 Déc 2020, 13:51
rebonjour,
on pose , pour
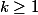
:
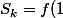+f(2)+...+f(k))
On a la minoration suivante:
+f(2)+...+f(k) \geq 1+2+..+k \geq \dfrac{k(k+1)}{2})
On peut voir cette minoration en dessinant les images f(i) , de coordonnées entières, sur un axe gradué et on minore la somme en "tassant vers la gauche " toutes les images à partir de 1, sur l'axe gradué.
On pose
}{k^2})

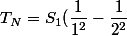+...+S_k(\dfrac{1}{k^2}-\dfrac{1}{(k+1)^2})+..+S_N(\dfrac{1}{N^2}))
en minorant
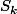
par
}{2})
^2} +\dfrac{S_N}{N^2})
(2k+1)}{2k^2 (k+1)^2})
or
(2k+1)}{2k^2 (k+1)^2} \sim \dfrac{2k^3}{2k^4} \sim \dfrac{1}{k})
quand k tend vers l'infini.
Donc la série
 /n^2;T_n))
est divergente vers

Modifié en dernier par mathelot le 30 Déc 2020, 11:58, modifié 1 fois.
-
Agouraptor
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Oct 2018, 19:54
-
 par Agouraptor » 28 Déc 2020, 16:57
par Agouraptor » 28 Déc 2020, 16:57
Merci beaucoup pour ta réponse ! Bien vu pour la transformation d'Abel, je n'y aurai pas pensé !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
. Merci en avance de vos réponses.