Une limite d'applications linéaires

[euler21]

Bonsoir
on se place dans un ev E de dimension finie non nulle et on considère un endomorphisme f non colinéaire avec l'identité I tel que f²=1/2(f+I)
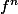
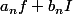
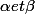
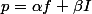
Par récurrence on démontre que = et que les deux suites convergent respectivement vers et que l'application est un projecteur.
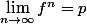
Ma question c'est que vu qu'on est dans un espace de dimension finie et qu'on peut le munir d'une norme. D'abord est ce qu'on peut dire que ?? et si c'est le cas est ce qu'il y a une interprétation topologique de ce résultat : la limite est un projecteur

[mathelot]

Bonsoir
D'abord est ce qu'on peut dire que

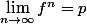
bah oui, appliquer la propriété d'une norme


2)
avec une norme sous-multiplicative , f semble contractante

3)
la suite des sous espaces
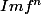
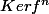
est décroissante et croissante
donc sans doute stationnaire en dimension finie