Une intégrale généralisée pas sympa...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
taskienne
- Messages: 4
- Enregistré le: 04 Juil 2007, 15:43
-
 par taskienne » 04 Juil 2007, 16:10
par taskienne » 04 Juil 2007, 16:10
Salut, :zen:
Encore moi, toujours en révision... :cry: Un petit problème sur une intégrale généralisée :
Intégrale de 0 à Pi/2 de sin(x) . ln (sin(x))...
Bien sur elle converge, en 0 c'est équivalent à x.ln(x) -->0 et en Pi/2 celà prend pour valeur 0... :zen:
Après pour ce qui est de la valeur... :marteau: Mr Texas 92 donne ln(2) - 1 en moins de 3 secondes... :hum: Mais je n'y arrive pas...
Alors si vous avez le truc, merci... :happy2:
A+ Task' :zen:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Juil 2007, 16:29
par Nightmare » 04 Juil 2007, 16:29
Salut :happy3:
C'est du changement de variable à volonté ça non?
On pote x=2t :
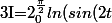)dt=2\[\Bigint_{0}^{\frac{\pi}{4}} ln2dt+\Bigint_{0}^{\frac{\pi}{4}} ln(sin(t))dt+\Bigint_{0}^{\frac{\pi}{4}} ln(cos(t))dt\])
On pose

:
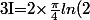+\Bigint_{0}^{\frac{\pi}{4}} ln(sint)dt-\Bigint_{\frac{\pi}{2}}^{\frac{\pi}{4}} ln(sin(u))du\]=2\[\frac{\pi}{4}ln2+\Bigint_{0}^{\frac{\pi}{2}} ln(sint)dt\]=\frac{\pi}{2}ln(2)+2I)
Finalement :
)
:happy3:
-
taskienne
- Messages: 4
- Enregistré le: 04 Juil 2007, 15:43
-
 par taskienne » 04 Juil 2007, 16:38
par taskienne » 04 Juil 2007, 16:38
Salut,
Merci mais... :triste: C'est sin(x).ln(sin(x)) que je cherche à intégrer et non ln(sin(x))... :id:
Enfin peu être que j'ai mal compris... :happy2:
A+ Task' :id:
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 04 Juil 2007, 16:43
par abcd22 » 04 Juil 2007, 16:43
Bonjour,
Une intégration par parties en dérivant le logarithme ça donne quoi ?
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 04 Juil 2007, 16:44
par kazeriahm » 04 Juil 2007, 16:44
tu peux intégrer par partie en integrant le sin et en dérivant ln(sin) je pense que c'est plutot sympa
-
taskienne
- Messages: 4
- Enregistré le: 04 Juil 2007, 15:43
-
 par taskienne » 04 Juil 2007, 16:53
par taskienne » 04 Juil 2007, 16:53
Et bien pour l'IPP le problème c'est que le premier terme qui est :
-cos(x).ln(sin(x))
en Pi/2 pas de problème ça fait 0...
mais en 0 ça donne plus l'infini... :hum:
Enfin bon si vous trouver chapeau, j'y ai passer 4h avec IPP, changement de variables... Etc... Mais pourtant ma calculatrice trouve ln(2) -1... :dodo:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Juil 2007, 17:42
par Nightmare » 04 Juil 2007, 17:42
Alors pose que ton intégrale est une limite avec une borne qui tend vers 0 !
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 04 Juil 2007, 18:01
par kazeriahm » 04 Juil 2007, 18:01
oui tu intègre entre epsilon et Pi/2, tu fais ton IPP, tu calcules tout et tu fais tendre ensuite epsilon vers 0
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 04 Juil 2007, 18:03
par Joker62 » 04 Juil 2007, 18:03
Pour ma part cette intégrale je l'ai vue avec le changement de variable de Nightmare :)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 05 Juil 2007, 11:46
par Pythales » 05 Juil 2007, 11:46
L'intégrale indéfinie donne, en posant
=u)
et
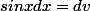
:
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 05 Juil 2007, 12:39
par Pythales » 05 Juil 2007, 12:39
En posant
)
et
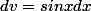
on trouve facilement pour l'intégrale indéfinie
+ln(tg \frac{x}{2})+cosx)
soit en développant
)-cosx.ln(cos(x/2))+ln(sin(x/2))-ln(cos(x/2))+cosx)
Pout

l'expression vaut

et pour

elle vaut
-1+lim_{x \rightarrow 0}(1-cosx) ln(sin(x/2)))
Un DL de cette expression montre que sa valeur est

ce qui donne
-1)
pour la valeur de l'intégrale
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
