Une inéquation récurrente
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 24 Nov 2019, 08:39
par Dacu » 24 Nov 2019, 08:39
Bonjour à tous,
Résoudre l'inéquation récurrente
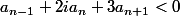
où
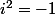
.
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 24 Nov 2019, 10:15
par tournesol » 24 Nov 2019, 10:15
je n'ai pas le temps mais le sujet est plaisant pour son originalité .
on peut poser
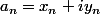
puis resoudre l'equation qui correspond a la condition d'appartenance à

, puis avec les suites obtenues , resoudre l'inéquation récurrente .
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 24 Nov 2019, 13:55
par tournesol » 24 Nov 2019, 13:55
Sont libres x0 , x1 , y0 , et y1 .
Ensuite , les parties imaginaires sont determinées par
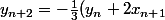)
,
et les parties réelles sont conditionnées par
)
Après résolution , on obtient:
^n}{3^n}y_0+\sum_{k=1}^n (-1)^k\frac{2}{3^k}x_{2n+1-2k})
^n}{3^n}y_1+\sum_{k=1}^n (-1)^k\frac{2}{3^k}x_{2n+2-2k})
On obtient des relations analogues pour le conditionnement.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 25 Nov 2019, 05:52
par Dacu » 25 Nov 2019, 05:52
tournesol a écrit:Sont libres x0 , x1 , y0 , et y1 .
Ensuite , les parties imaginaires sont determinées par
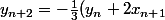)
,
et les parties réelles sont conditionnées par
)
Après résolution , on obtient:
^n}{3^n}y_0+\sum_{k=1}^n (-1)^k\frac{2}{3^k}x_{2n+1-2k})
^n}{3^n}y_1+\sum_{k=1}^n (-1)^k\frac{2}{3^k}x_{2n+2-2k})
On obtient des relations analogues pour le conditionnement.
Bonjour,
Je ne comprends pas , c'est trop compliqué , s'il vous plait donnez des détails! Quelle est l'expression de

?Merci beaucoup!
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Yezu
- Membre Relatif
- Messages: 335
- Enregistré le: 14 Fév 2018, 12:29
-
 par Yezu » 25 Nov 2019, 08:35
par Yezu » 25 Nov 2019, 08:35
Salut,
@tournesol je ne sais pas comment tu trouves la motivation de répondre à Dacu qui n'en a absolument rien à fouttre de toutes les remarques que les vétérans d'ici lui bassinent ^^
On attend le classique :
"Certains disent que ... " (lien wolfram).
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 25 Nov 2019, 14:12
par tournesol » 25 Nov 2019, 14:12
Ma motivation vient de mon interet pour ce type d'exo que je n'avais jamais rencontré .
Quand à l'expression de an , il n'y en a pas car xn n'est mas déterminable mais conditionne par une inégalité .
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 27 Nov 2019, 07:41
par Dacu » 27 Nov 2019, 07:41
tournesol a écrit:Quand à l'expression de an , il n'y en a pas car xn n'est mas déterminable mais conditionne par une inégalité .
Bonjour,
Je ne comprend pas!Mon raisonnement:
L'inéquation récurrente
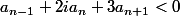
où
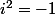
il peut être écrit comme étant l'équation
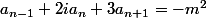
où
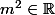
et
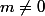
. Mon raisonnement est-il correct?Merci beaucoup!
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 27 Nov 2019, 07:46
par tournesol » 27 Nov 2019, 07:46
ton idée est de parametrer les solutions . Je la trouve bonne et je n'y avait pas pensé .
je vais donc reprendre l'exo .
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 27 Nov 2019, 08:27
par tournesol » 27 Nov 2019, 08:27
Merci pour ton aide.Le paramétrage est ce qu'il fallait faire .
La solution générale de l'équation
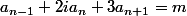
est
^n+B(i/3)^ n+\frac{m}{4+2i})
avec A et B décrivant

.
La solution génerale de ton inéquation s'obtient à partir de la précédente lorsque m décrit ]-

;0[
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 27 Nov 2019, 17:23
par Dacu » 27 Nov 2019, 17:23
tournesol a écrit:Merci pour ton aide.Le paramétrage est ce qu'il fallait faire .
La solution générale de l'équation
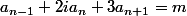
est
^n+B(i/3)^ n+\frac{m}{4+2i})
avec A et B décrivant

.
La solution génerale de ton inéquation s'obtient à partir de la précédente lorsque m décrit ]-

;0[
Bonsoir,
Avec plaisir!
Je ne pense pas qu'il était nécessaire de changer l'équation proposée par moi....
L'équation proposée
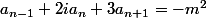
où
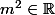
et
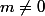
et donc la solution génerale de mon inéquation est
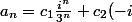^n-(\frac{1}{5}-\frac{i}{10})m^2)
.Merci beaucoup!
Cordialement,
Dacu
Modifié en dernier par
Dacu le 28 Nov 2019, 16:03, modifié 2 fois.
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 27 Nov 2019, 17:30
par tournesol » 27 Nov 2019, 17:30
OK Dacu mais m appartient à
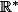
-
mathelot
 par mathelot » 27 Nov 2019, 17:50
par mathelot » 27 Nov 2019, 17:50
m dépend de n. Il vaudrait mieux écrire
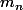
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 27 Nov 2019, 19:28
par tournesol » 27 Nov 2019, 19:28
Bien sur Mathelot . Je me fait vieux .
Exo à reprendre .
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 28 Nov 2019, 08:00
par Dacu » 28 Nov 2019, 08:00
mathelot a écrit:m dépend de n. Il vaudrait mieux écrire
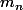
Bonjour,
Je ne comprend pas!Je ne pense pas que

dépend de

et je dis que
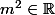
*.Merci beaucoup!
Cordialement,
Dacu
Modifié en dernier par
Dacu le 28 Nov 2019, 16:09, modifié 5 fois.
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 28 Nov 2019, 08:05
par Dacu » 28 Nov 2019, 08:05
Bonjour,
tournesol a écrit:Bien sur Mathelot . Je me fait vieux .
Exo à reprendre .
Non!Le paramètre

ne dépend pas du paramètre

, car
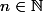
.
tournesol a écrit:OK Dacu mais m appartient à
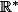
Oui!Tu as raison!J'ai tout corrigé!

Merci beaucoup!
Cordialement,
Dacu
Modifié en dernier par
Dacu le 28 Nov 2019, 16:13, modifié 2 fois.
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 28 Nov 2019, 16:11
par Dacu » 28 Nov 2019, 16:11
Bonne soirée à tous,
Quel est le premier terme de la chaîne?Quelle est la restriction de paramètre

?
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
,
Après résolution , on obtient:
^n}{3^n}y_0+\sum_{k=1}^n (-1)^k\frac{2}{3^k}x_{2n+1-2k})
est
avec A et B décrivant
.
;0[