Une équation fonctionnelle

[Celph]

Bonjour à tous,

Voici un problème sur lequel je bute,
Pour T l'ensemble des fonctions g continues de R dans R telles que pour tout (x,y) dans R², on a
g(x+y) + g(x-y) = 2 [g(x)g(y)]

On montre facilement que T est non vide et que pour g dans T, on a g(0) valant 0 ou 1.
Cela dit, ayant supposé que g(0)=1, je n'arrive pas à prouver que g est dérivable sur R.

Avez-vous des idées ?
Merci d'avance ! :briques:

[Nightmare]

Bonjour

En vrac :

Les fonctions ch et cos sont solutions de l'équation.

Si l'on montre que f est 2 fois dérivables, on montrera qu'elle vérifie l'équation f''(x)=f(0).f(x) dont on sait trouver les solutions.

En posant x=0 on montre que f est impaire.

[Celph]

Bonjour Nightmare,

As-tu une idée de la méthode à employer pour prouver la dérivabilité de g ?

[Flodelarab]

Bonjour

En vrac :

Les fonctions ch et cos sont solutions de l'équation.

Si l'on montre que f est 2 fois dérivables, on montrera qu'elle vérifie l'équation f''(x)=f(0).f(x) dont on sait trouver les solutions.

En posant x=0 on montre que f est impaire.

Le fait d'avoir 2 exemples faciles, ne prouve aucunement la dérivabilité sur R.

Tout l'énoncé est la ? Ne peut on pas calculer le nombre dérivé en tout point ?

[Nightmare]

Le fait d'avoir 2 exemples faciles, ne prouve aucunement la dérivabilité sur R.

Je n'ai jamais dit ça ...

[Flodelarab]

est il juste de dire:

lim(h->0) [(g(x0+h)-g(x0))/h] + lim(h->0) [(g(x0-h)-g(x0))/h]
= lim(h->0) [(g(x0+h)+g(x0-h)-2g(x0))/h]
= lim(h->0) [(2g(x0)g(h)-2g(x0))/h]
= lim(h->0) [2g(x0)*(g(h)-1)/h]

si g(0)=0, pas de probleme. La fonction g n'est pas dérivable sur R car le nombre dérivé tend vers l'infini

si g(0)=1 .... c encore indéterminé.

G ptet loupé une achtuce. Qu'en pensez vous?

[Nightmare]

Si g(0)=0 on peut montrer que g est la fonction nulle.

[Yipee]

C'est un exercice classique (mais très difficile s'il est posé sans indications). Je vous en propose donc quelques unes :
1 - Montrer que si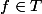 alors, pour tout réel a la fonction est encore dans T.
2 - On suppose que f(0)=1 et que f s'annule. On veut montrer que f est de la forme . Pour cela on considère la borne inférieure de (après avoir montré quelle existe) et l'ensemble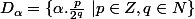

Bonne chance...

[cesar]

si g(x) n'est pas identiquement nulle, il existe X0 tel que g(x0) different de 0.

donc si on pose y= 0 et x=x0, on a :

g(x0+0)+g(x0-0)= 2*g(x0)*g(0)

soit 2*g(x0)=2*g(x0)*g(0) et comme g(x0) non nul, il vient g(0)=1

si g(x) est identiquement nulle, il est facile de voir que c'est aussi une solution

autre point :

si y tel que g(y) non nul:

g(0+y)+g(0-y)=2*g(0)*g(y)
et comme g(0)=1 :
g(-y) = g(y)
g est paire...

[Vedeus]

Je prouve que toute solution est deux fois dérivable. Pour cela, je considère
une solution , supposée non identiquement nulle sur .
Il existe alors un couple tel que
. On note cette intégrale.

Pour tout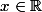 , on déduit de l'équation
vérifiée par que

(en intégrant par rapport à la seconde variable)

d'où


En choisissant une primitive de , on obtient que pour tout réel :


On en déduit facilement que est dérivable, puis que est deux fois dérivable, et enfin que est deux fois dérivable.

Remarque : cette astuce est tout à fait classique lorsqu'il s'agit de résoudre
des équations fonctionnelles.

[Celph]

Je butais au même point que Flodelarab,
J'étais donc loin de la solution proposée par Vedeus.
Merci de votre aide ! :id:

[cesar]

finissons le travail : on sait que g se derive au moins 2 fois.

g(x+y) +g(x-y) = 2 g(x)*g(y)
si on dérive 2 fois par rapport à x, il vient :

g''(x+y)+g''(x+y) = 2 * g"(x)*g(y)

si on derive 2 fois par rapport à y, il vient :

g''(x+y)+g''(x+y) = 2 * g(x)*g''(y)

donc par élimination :

g(x)*g''(y) = g(y)*g''(x)
et si on pose y=y0 fixé : g''(x) = [g''(y)/g(y)]*g(x)
si on pose k, tel que k*k = g''(y)/g(y)
alors g(x) = A*exp(k*x) + B*exp(-k*x)

on sait dejà que g(0)=1
si on derive par rapport à y une fois
g(x+y) +g(x-y) = 2 g(x)*g(y) devient
g'(x+y)-g'(x-y) = 2*g(x)*g'(y)

en prenant y = 0, on obtient 0=g(x)*g'(0) pour tout x, donc g'(0)=0..

et comme g(0) = A+ B = 1
et g'(0) = k*A -K*B = 0
on en deduit A=B=1/2...
g(x) = ch(kx) si k reel
g(x) = cos(kx) si k est imaginaire
les formules de trigo permettent de verfier que la relation g(x+y) +g(x-y) = 2 g(x)*g(y) est valable quelque soit la valeur de k...