Une équation avec un paramètre

[Dacu]

Bonjour tout le monde,

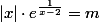
Pour quelles valeurs du paramètre , l'équation a trois solutions réelles et distinctes?Merci très beaucoup!

Cordialement,

Dacu

[pascal16]

je te fais 66% de l'exo.
si m<0 : pas de solution
si m=0 : 1 solution
il ne te reste que le cas m>0

Pourquoi ne pas faire comme en lycée où l'on dérive, on trouve les zéros de la dérivée, on fait un tableau de variation (sans oublier le cas x=0, x=2 et le les limites), on regarde les extremums, et on conclue par le TVI.

[Dacu]

je te fais 66% de l'exo.
si m<0 : pas de solution
si m=0 : 1 solution
il ne te reste que le cas m>0

Pourquoi ne pas faire comme en lycée où l'on dérive, on trouve les zéros de la dérivée, on fait un tableau de variation (sans oublier le cas x=0, x=2 et le les limites), on regarde les extremums, et on conclue par le TVI.

Bonsoir,

Il est évident que .
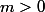
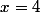
Soit , alors pour est obtenu un maximum et pour est obtenu un minimum , ce qui signifie que pour .Mon raisonnement est-il correct?Merci très beaucoup!

Cordialement,

Dacu

[pascal16]

graphiquement, oui, avec chaque borne ouverte
perso, je ferais un tableau de variations, il faut les limites en -oo, 2-, 2+ et +oo.
il faut justifier par le tvi à chaque fois le nombre de solutions

[Dacu]

graphiquement, oui, avec chaque borne ouverte
perso, je ferais un tableau de variations, il faut les limites en -oo, 2-, 2+ et +oo.
il faut justifier par le tvi à chaque fois le nombre de solutions

Bon matin,

J'ai compris et pour dessiner le graphique de fonction , nous devons voir les valeurs de la cette fonction et en certains points avec le tableau de variations spécifié par vous. Encore une fois , merci très beaucoup!

Cordialement,

Dacu