Y'a 36 façons de voir le chmilblick. Si tu est pas super familer avec la notion de variétés, on peut le voir uniquement en terme de fonctions :
L'ensemble
)
des matrices orthogonale, c'est l'ensemble des matrices telles que
\!=\!I_3)
où
\to{\mathcal M}_3({\mathbb R})\,;\,M\mapsto {}^t\!MM)
et avec ce point de vue, ton problème s'énonce de façon archi. classique sous la forme :
Déterminer le max de ) sous la contrainte
sous la contrainte \!=\!I_3)
.
Et dans cas, comme dans celui des maximum
sans contraintes de fonctions de plusieurs variables, il y a une notion de "point critiques" qui sont les "candidats potentiels" pour être des min/max locaux :
Si on se place en un point

(qui ici est une matrice, mais on s'en fout) tel que
\!=\!I_3)
et qu'on fait une "petite perturbation"

on a
\!\approx\!\psi(M)\!+\!d_\psi(M).H)
où
.H)
est la différentielle de

au point

appliquée au vecteur

. Donc pour que
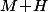
soit lui aussi (approximativement) dans
)
, il faut que
.H\!=\!0)
c'est à dire que

soit dans le noyau
))
(c'est ce noyau qu'on appelle "espace tangent à
)
au point M"). Ensuite, concernant la fonction à maximiser, on a aussi
\!\approx\!\varphi(M)\!+\!d_\varphi(M).H)
et donc pour que

soit un candidat potentiel pour être un max ou un min local (sous contrainte), il faut que pour tout
))
on ait
.H)
(sinon, suivant cette direction

on pourrait faire augmenter/diminuer

en restant dans
)
) donc en résumé, il faut que
)\subset\ker(d_\varphi(M)))
(*).
Et pour revenir au cas qui nous intéresse, vu que

est linéaire, on a
\!=\!\varphi)
pour tout point

et concernant

, on a :
\!=\!{}^t(M\!+\!H)(M\!+\!H)\!=\!{}^t\!M M\!+\!{}^t\! M H\!+\!{}^t\!H M\!+\!{}^t\!HH\approx\psi(M)\!+\!{}^t\!MH\!+\!{}^t\!HM)
pour

petit.
Donc
.H\!=\!{}^t\!MH\!+\!{}^t\!HM\!=\!{}^t\!MH\!+\!{}^t\!\big({}^tMH\big))
et donc
))
ssi
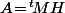
est antisymétrique (i.e.
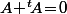
), c'est à dire
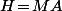
avec

antisymétrique. Donc dans ce cas, la condition en rouge ci dessus s'énonce sous la forme
\!=\!0)
pour toute matrice antisymétrique

.
(*) En temps que physicien, tu as sûrement déjà vu ce truc là qui, en terme calculatoire, s'énonce sous sous la forme de "
multiplicateurs de Lagrange" et je pense que le reste doit aussi évoquer des choses pour toi mais sans doute avec un formalisme différent.

