Trouver une limite

[Dinozzo13]

Bonsoir, je recherche actuellement un exercice guidé, me permettant de montrer et de trouver la limite de la suite suivante définie pour tout non nul par : .

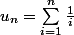
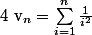
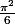
J'ai fait un exercice similaire ou j'ai trouvé que la suite définie pour tout non nul par : converge vers mais je ne pense pas si à partir de ce résultat, je peux en déduire quelque chose de la limite de la suite u (je dirai même, que je ne crois pas).

MErci d'avance pour votre aide car la limite de cette somme m'intrigue depuis 2-3 ans et j'aimerais bien la trouver par moi-même :++:

[Sylviel]

La méthode la plus simple consiste à faire une comparaison série-intégrale (en comparant 1/n et la valeur de 1/x entre n et n+1, et entre n-1 et n). Bon courage.

P.S : pour plus de précisions sur le sujet cherche "constante d'Euler".

[Nightmare]

Hello,

Tu as bu Dinozzo? Tu as posté la même question [url="http://www.maths-forum.com/somme-d-inverses-113285.php"]ici[/url] il y a quelques jours. La réponse à ta question se trouve dans cet autre topic.

[Arnaud-29-31]

Tu peux regarder du coté de la fonction dzeta de Riemann ... ta suite ne converge malheureusement pas.

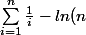Par contre tu pourra montrer que converge vers la constante d'Euler.


EDIT : Exact ... j'ai d'ailleurs donné la même réponse lool

[Dinozzo13]

Ok Sylviel, je vais taper ça sur internet :++:

@Nightamre : Non :ptdr: je bois vraiment très peu, je déteste l'alcool, pis il me viendrait pas l'idée de boire pendant le boulot :ptdr: , mais en ce moment je suis particulièrement fatigué, un truc de malade, et j'oublie donc souvent des trucs (comme faire mon anglais par exemple :ptdr:).

Mais je me suis demandé justement si je n'avait pas déjà posé cette question, et je me suis trompé.

@Arnaud : La suite u ne converge pas ! Ca me paraît bizarre, comment se fait-il alors que v converge ?
Comment montrer alors que u ne converge pas ?

[Sylviel]

Regarde l'autre post, il y a toutes les réponses à ces questions...
La série ne converge pas car 1/n décroit trop lentement... Mais regarde l'autre post Ben t'y détaille comment faire, et plein de gens te donnent plein d'indics supplémentaires ;-)

[Nightmare]

Ma question n'en était pas vraiment une, je me doute que tu n'es pas saoul (encore que finalement, j'en sais rien)

L'argument le plus "simple" pour dire que la suite diverge est l'argument donné par Ben : Il n'est pas trop difficile de montrer qu'une suite qui converge voit ses termes se rapprocher de plus en plus (et de manière uniforme qui plus est). On dit que la suite est de Cauchy.

Ici, un calcul rapide permet de minorer la différence |u(2n)-u(n)| par 1/2, ce qui veut dire que quel que soit n, la distance entre u(2n) et u(n) n'est jamais inférieure à 1/2, donc en particulier, elle ne sera jamais aussi petite que l'on veut...