Trouver une base

[nico2b]

Bonjour, il nous est demandé de trouver une base de W qui est l'espace engendré par les polynômes v1 = t³ - 2t² + 4t + 1 ; v2 = 2t³ - 3t² + 9t - 1 ; v3 = t³ + 6t - 5 et v4 = 2t³ - 5t² + 7t + 5 mais je ne sais vraiment pas comment m'y prendre...

Il faut trouver une famille libre et génératrice mais bon :hein:

Auriez-vous des pistes?

Merci beaucoup

[aviateurpilot]

eassaye de trouver une base de W' qui est l'espace engendré par les 4-uplets:
v1 =(1,-2,4,1)
v2 = (2,-1,9,-1)
v3 = (1,0,6,-5)
v4 = (2,-5,7,5)

[nico2b]

Comment on s'y prend pour trouver une base? Y a-t-il une marche à suivre?
Parce que je ne vois vraiment pas comment commencer...

Merci pour ton aide

[kazeriahm]

reviens a la définition :

W est engendré par tes 4 polynomes, donc la famille (v1,v2,v3,v4) est génératrice de W, puisque par définition, tout polynome de W s'écrit comme combinaison linéaire de v1,v2,v3 et v4.

ensuite essaye de voir si (v1,v2,v3,v4) est libre. Si c'est le cas, cette famille étant livre et génératrice de W, c'en est une base

[aviateurpilot]

Comment on s'y prend pour trouver une base? Y a-t-il une marche à suivre?
Parce que je ne vois vraiment pas comment commencer...

Merci pour ton aide

desolé, je ne suis pas tres fort dans ce genre d'exo algorithmique.
mais je peux te dire que v1,v2,v3 libre

[nico2b]

Ok ce n'ai pas grave merci de m'avoir aidé quand même :we:

Au cour j'ai souvenir d'une méthode utilisé qui consisterai à faire ceci :

suposer qu'on a 0 = xv1 + yv2 + zv3 + sv4 avec x,y,z,s mais je ne vois pas où celà nous menerais pour trouver une base... Et pourquoi faut-il tout égaler à zero.

[kazeriahm]

la famille v1, v2, v3,v4 est libre (par définition) ssi
pour tout (t,x,y,z) dans R^4, (t*v1+x*v2+y*v3+z*v4=0) => (t=x=y=z=0)

[nico2b]

Ok kazeriahm je vais regarder à ça et reposterai
Merci de ton aide

[aviateurpilot]

calcule les determinant de la matrice
(1,-2,4,1)
(2,-1,9,-1)
(1,0,6,-5)
(2,-5,7,5)
s'il est alors [(t*v1+x*v2+y*v3+z*v4=0) => (t=x=y=z=0)] et dans ce cas v1,v2,v3,v4 base.
sinon alors v1,v2,v3 est une base de W

[emdro]

Nico,

Ta famille n'est pas libre, je te laisse le découvrir. Cela prouve que ta famille est liée, donc la dimension est <4.

Dans ce cas, trouve une relation linéaire entre les polynômes, on pourra décider ensuite lequel éliminer.

Donne nous ta relation linéaire lorsque tu l'auras trouvée;

[kazeriahm]

oui aviateurpilot c'est une autre méthode, surement plus rapide, mais je crois que nico2b a besoin de voir les choses calmement et je suis pas sur qu'il voit le lien avec ce que tu dis

[nico2b]

Voici le détail de mes calculs :

x (t³-2t²+4t+1) + y (2t³-3t²+9t-1) + z(t³+6t-5) + s(2t³-5t² + 7t+5)= 0
[x+2y+z+2s] t³ + [-2x - 3y-5s] t² + [4x+9y+6z+7s]t + [x-y-5z+5s] = 0

Donc j'obtient le système:



Après échelonnage je trouve :



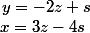
Donc ça vaut 0 ssi x = 3z - 4s et y = -2z + s donc la famille n'est pas libre...
Jusque là ça va?

Merci à tous pour votre aide :happy2:

-Je suis de retour-

[aviateurpilot]

v1 =(1,-2,4,1)
v2 = (2,-1,9,-1)
v3 = (1,0,6,-5)
est liée, alors
v1' =(1,-2,4)
v2' = (2,-1,9)
v3' = (1,0,6)
est liée
donc determenant de v1',v2',v3' nul (mais il est egale à -6+4x6-18+4=4)
donc v1,v2,v3 libre.
donc dim(W)>=3

donc tu n'a que calculer le determinant de
(1,-2,4,1)
(2,-1,9,-1)
(1,0,6,-5)
(2,-5,7,5)
s'il est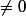 , v1,v2,v3,v4 est une base
dim(w)<=3
et en plus v1,v2,v3 c'est une base

sauf si j'ai fait une faute dans les calcule de det

[kazeriahm]

je n'ai pas regardé les calculs ni de l'un ni de l'autre mais vos résultats sont incompatibles

[aviateurpilot]

je n'ai pas regardé les calculs ni de l'un ni de l'autre mais vos résultats sont incompatibles

je sais, c'est pour cela que j'ai dit sauf si j'ai fait une faute dans les calcule de det, lol

edit: j'ai pris v2 = (2,-1,9,-1) a la place de v2=(2,-3,9,-1)

[emdro]

Nico,

Parfait.

Tu sens donc que le rang de la famille est deux.
De manière plus détaillée:
Si on choisit z=1 et s=0 cela donne x=3 et y=-2
soit: 3v1-2v2+v3=0 et donc v3=-3v1+2v2

Si tu prends z=0 et s=1 cela donne x=-4 et y=1
soit: -4v1+v2+v4=0 et donc v4=4v1-v2

C'est maintenant clair: on a exprimé v3 et v4 comme combinaisons linéaires de v1 et v2. Ces vecteurs n'ajoutaient donc rien, ils peuvent être retirés.
d'ou dim inférieure ou égale à 2.

C'est facile de voir que la famille (v1,v2) est libre (sinon, on verrait immédiatement le lien de proportionnalité). Donc cette famille (génératrice) est une base.

C'est clair?

[nico2b]

J'avou que j'ai du mal à tout comprendre avec la méthode des déterminants lol
On ne peut pas faire autrement? surtout que tout ce qui concerne les matrices vient après dans le cour...

Enfin je veux bien le calculer mais j'arrive pas à comprendre pourquoi, si le det est différent de 0, alors on aura une base.

Et à partir de ce que j'ai fait on ne sait rien retiré de plus? Je vois que (v1, v2, v3, v4) est lié mais je ne sais pas vers où m'orienter pour la suite

On a (3z-4s) v1 + (-2z+s)v2 + zv3 + sv4 = 0 (sauf erreur de calcul de ma part)

Merci à tous

[aviateurpilot]

emdro, tu dit que 3v1-2v2+v3=0
avec ,
v1 =(1,-2,4,1)
v2 = (2,-1,9,-1)
v3 = (1,0,6,-5)
mais c'est faux

[nico2b]

Oui c'est très clair :happy2:
Vraiment merci pour ces explications

Donc pour résumé, pour trouver une base pour ce genre d'énoncé,

1) on regarde si la famille génétracide de l'espace est libre

- si oui : ok c'est une base
- si non : on regarde quel vecteur est combinaison linéaire d'autre et on peut supprimer cela.

2) On vérifie bien si les vecteurs restants sont linéaire... Et on a notre base :happy2:

J'ai bien compris? lol

Merci encore

[nico2b]

Si v2 représente les coordonées du polynomes, alors il y aurait une erreur dans v2 = (2, -3, 9, -1) c'est -3 au lieu de -1 aviateurpilot