Bonjour à tous,
J'ai un petit problème à vous poser que je n'arrive pas à résoudre et qui me sortirai une épine du pied pour là où je travaille.
J'ai A, B, C et D réels connus et (x,y,z) R³ sachant x,y,z compris entre 0 et 1 (ce sont des pourcentages).
Comment puis-je faire pour travailler la solution optimale pour x,y,z tel que xA+yB+zC = D?
Merci par avance pour ceux qui pourront m'aider !
ps : Pour ceux qui connaissent un outil capable de résoudre ce genre de problème, je prends !
Trouver la meilleure solution sachant ....
6 messages
- Page 1 sur 1
En gros je veux trouver le meilleur arbitrage possible pour x,y et z.
Si on considère par exemple que A, B et C sont des sommes que vont toucher des gens, et D le total avec A < B < C
Pour qu'aucun ne soit déçu, je cherche à trouver les meilleurs coefficients x,y et z (c a d les plus hauts) tout en conservant le total. Les coefficients ne peuvent être tous égal à 1 sinon A+B+C n'est pas égal à D.
Je vais donner quelques chiffres pour que cela soit plus parlant
Disons A = 2000, B = 2000, C = 3000 et le total D = 5000. Quels sont les meilleurs coefficients x,y,z tel que xA + yB + zC = 5000 ? En gros, quel est le meilleur arbitrage possible (le plus élevé, le plus équitable)?
Si on considère par exemple que A, B et C sont des sommes que vont toucher des gens, et D le total avec A < B < C
Pour qu'aucun ne soit déçu, je cherche à trouver les meilleurs coefficients x,y et z (c a d les plus hauts) tout en conservant le total. Les coefficients ne peuvent être tous égal à 1 sinon A+B+C n'est pas égal à D.
Je vais donner quelques chiffres pour que cela soit plus parlant
Disons A = 2000, B = 2000, C = 3000 et le total D = 5000. Quels sont les meilleurs coefficients x,y,z tel que xA + yB + zC = 5000 ? En gros, quel est le meilleur arbitrage possible (le plus élevé, le plus équitable)?
re,
ben la on cherche pas a la maximiser (ou alrs jai mal capté) vu que xA+yB+zC=D. On veut maximiser x et y et z.
Voila les contraintes :
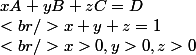
On peut se ramener a deux variables
C - D = 0)
On peut simplement exprimer y en fonction de x
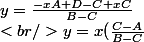 + \frac{D - C}{B - C})
On a la (sauf boulette) tous les couples solutions (x,y), moyennant x positif et y aussi
Ensuite, pour les choisir, il faudrait que x = y = z, la i sont bien equitables. Donc j'ai envie de dire que la meilleure solution est celle qui minimise la variance entre x,y et z
cad posons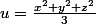 , alors on cherche min(u)
, alors on cherche min(u)
sous les contraintes
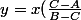 + \frac{D - C}{B - C}\\<br />y = xK+H) , avec
, avec 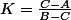 et
et 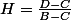

donc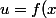)
La on peut chercher a optimiser u,
 = f(x))
En exprimant z en fonction de y,x puis tout de x et y en fonction de x
On a des termes en carré, en dérivant des termes en 1, donc a priori on a une droite.
On est capable de savoir pour quel valeur de x u est minimale. Il s'agit de trouver le x en suivant la fonction, tel qu'il satisfait les contraintes.
Ca devient un probleme d'optimisation linéaire :
on a

Enfin, je pense. Apres c'est du bricolage custom, ya surement des méthodes mieux.
EDIT : boulette sur la fin, mais la c'est lheure (ou plus lheure?) d'aller en cours!
Edit 2 : je termine cque javais commencé:
on a aussi les cond y < 1, et z < 1
Edit 3 : jviens de voir que c'est un cas de programmation quadratique. Vu que la fonction objective est avec termes carrés et les contraintes sont linéaires
tu cherches à la maximiser
ben la on cherche pas a la maximiser (ou alrs jai mal capté) vu que xA+yB+zC=D. On veut maximiser x et y et z.
Voila les contraintes :
On peut se ramener a deux variables
On peut simplement exprimer y en fonction de x
On a la (sauf boulette) tous les couples solutions (x,y), moyennant x positif et y aussi
Ensuite, pour les choisir, il faudrait que x = y = z, la i sont bien equitables. Donc j'ai envie de dire que la meilleure solution est celle qui minimise la variance entre x,y et z
cad posons
sous les contraintes
donc
La on peut chercher a optimiser u,
En exprimant z en fonction de y,x puis tout de x et y en fonction de x
On a des termes en carré, en dérivant des termes en 1, donc a priori on a une droite.
On est capable de savoir pour quel valeur de x u est minimale. Il s'agit de trouver le x en suivant la fonction, tel qu'il satisfait les contraintes.
Ca devient un probleme d'optimisation linéaire :
on a
Enfin, je pense. Apres c'est du bricolage custom, ya surement des méthodes mieux.
EDIT : boulette sur la fin, mais la c'est lheure (ou plus lheure?) d'aller en cours!
Edit 2 : je termine cque javais commencé:
on a aussi les cond y < 1, et z < 1
Edit 3 : jviens de voir que c'est un cas de programmation quadratique. Vu que la fonction objective est avec termes carrés et les contraintes sont linéaires
la vie est une fête 
Salut,
Je pense qu'il y a un petit problème d'énoncé :
Pour que cela ait "mathématiquement" du sens, il faudrait, par exemple, que tu veuille que x+y+z soit maximum....
Je pense qu'il y a un petit problème d'énoncé :
mathématiquement, cette phrase n'est pas claire du tout : considère tu que x=0.2, y=0.4, z=0.4 est "meilleur" ou pas que x=0.3, y=0.3, z=0.3 ?glereun a écrit:...je cherche à trouver les meilleurs coefficients x,y et z (c a d les plus hauts)...
Pour que cela ait "mathématiquement" du sens, il faudrait, par exemple, que tu veuille que x+y+z soit maximum....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
