Trigonométrie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
antoine3617
- Membre Naturel
- Messages: 78
- Enregistré le: 30 Nov 2006, 10:55
-
 par antoine3617 » 09 Sep 2008, 20:41
par antoine3617 » 09 Sep 2008, 20:41
Bonjour,
Voici mon problème : je n'arrive pas à montrer que
 \gamma}}{2\sin{\frac{\gamma}{2}}})
Auparavant, je viens de calculer

en fonction de n et de

en posant

merci par avance
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 09 Sep 2008, 20:52
par izamane95 » 09 Sep 2008, 20:52
bonjour
essaye en utilisant les exponnentielles .....
c'est trivial en developpant Re(exp(.....
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 09 Sep 2008, 20:57
par izamane95 » 09 Sep 2008, 20:57
en fait ta somme de gauche c'est la
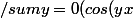))
=
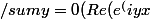))
=Re(somme(...))....
-
antoine3617
- Membre Naturel
- Messages: 78
- Enregistré le: 30 Nov 2006, 10:55
-
 par antoine3617 » 09 Sep 2008, 21:01
par antoine3617 » 09 Sep 2008, 21:01
en fait, mon idée était de remettre l'expression sous la forme a+ib pour ensuite prendre la partie réelle. Or c'est la catastrophe au niveau calculatoire.
Je pars de
\gamma}}{1-e^{i\gamma}})
qui correspond à la somme citée ci-dessus

mais ça me parait très compliqué au niveau calcul et pourtant je travaille avec des exponentielles
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 09 Sep 2008, 21:05
par izamane95 » 09 Sep 2008, 21:05
ah mais non c'est pas compliqué tu peux continuer ;en effet tu factorise par
/2})
-
mathelot
 par mathelot » 09 Sep 2008, 21:09
par mathelot » 09 Sep 2008, 21:09
izamane95 a écrit:ah mais non c'est pas compliqué tu peux continuer ;en effet tu factorise par
/2})
\gamma /2})
-
antoine3617
- Membre Naturel
- Messages: 78
- Enregistré le: 30 Nov 2006, 10:55
-
 par antoine3617 » 09 Sep 2008, 21:13
par antoine3617 » 09 Sep 2008, 21:13
mais ça ne va pas enlever la partie imaginaire au dénominateur, but recherché ? Pour moi, la seule solution est de multiplier par le conjugué au dénominateur et ce n'est pas très simple...
-
switch_df
- Membre Relatif
- Messages: 107
- Enregistré le: 21 Mar 2008, 17:20
-
 par switch_df » 09 Sep 2008, 21:14
par switch_df » 09 Sep 2008, 21:14
\sin\frac{t}{2}=\sin\frac{t}{2}+2\sin \frac{t}{2}\cos t+\ldots+2\sin \frac{t}{2}\cos nt=\ldots=\sin\left(n+\frac{1}{2}\right)t)
en utilisant que
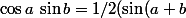-\sin(a-b)))
-
mathelot
 par mathelot » 09 Sep 2008, 21:14
par mathelot » 09 Sep 2008, 21:14
antoine3617 a écrit:mais ça ne va pas enlever la partie imaginaire au dénominateur, but recherché ? Pour moi, la seule solution est de multiplier par le conjugué au dénominateur et ce n'est pas très simple...
réfléchis. l'exponentielle est un morphisme
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 09 Sep 2008, 21:34
par izamane95 » 09 Sep 2008, 21:34
antoine3617 a écrit:mais ça ne va pas enlever la partie imaginaire au dénominateur, but recherché ? Pour moi, la seule solution est de multiplier par le conjugué au dénominateur et ce n'est pas très simple...
non mais c'est ce qu'on cherche a avoir ta partie imaginaire c'est le sinus machin que tu cherche a avoir ....
l'idée de depart c'etait de partir de la somme de gauche pour faire apparaitre apres le sinus machin en haut et en bas..
-
antoine3617
- Membre Naturel
- Messages: 78
- Enregistré le: 30 Nov 2006, 10:55
-
 par antoine3617 » 09 Sep 2008, 21:35
par antoine3617 » 09 Sep 2008, 21:35
oui, d'accord, mais quand je factorise par
\frac{\gamma}{2}})
ça ne colle pas et en plus je ne vois pas pourquoi factoriser ainsi dans ce cas
-
mathelot
 par mathelot » 09 Sep 2008, 21:39
par mathelot » 09 Sep 2008, 21:39
re,
il suffit d'utiliser l'identité remarquable:
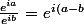})
après avoir factorisé le dénominateur.
-
antoine3617
- Membre Naturel
- Messages: 78
- Enregistré le: 30 Nov 2006, 10:55
-
 par antoine3617 » 09 Sep 2008, 21:50
par antoine3617 » 09 Sep 2008, 21:50
j'arrive à une soustraction au numérateur et au dénominateur donc l'identité me semble bizarre à utiliser ici...
-
mathelot
 par mathelot » 10 Sep 2008, 05:16
par mathelot » 10 Sep 2008, 05:16
-
antoine3617
- Membre Naturel
- Messages: 78
- Enregistré le: 30 Nov 2006, 10:55
-
 par antoine3617 » 10 Sep 2008, 08:24
par antoine3617 » 10 Sep 2008, 08:24
merci beaucoup, je vais travailler là-dessus immédiatement.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités