Trigonometrie

[Blisten]

voici l'ennoncé et ce que j'ai fait :

(racine(3)+1)cosx + (racine(3)-1)sinx + racine(3) - 1 = 0

j'ai commencer par passer racine(3)-1 de l'autre coté du signe egal puis j'ai divisé toute l'equation par (racine(3)+1)

j'optiens :

cosx + (racine(2)/2)sinx = -1

je bidouille le tout et j'optiens :

cosx + sin(pi/4)sinx = cos(pi)

mais arrivé a là je suis bloqué. je ne sais pas quoi faire.

soit passer cosx de l'autre coté du signe egal ce qui me donnerai cos(pi) - cosx

puis utiliser une formule de trigo :

cos(p)-cos(q) = -2 (sin( (p + q) /2 )sin( (p-q) /2 ))

et après je serai encore bloqué.

voilà si vous pouviez me donner un conseil

[fatal_error]

Salut,

peut-être peut-on essayer d'utiliser

[Blisten]

je ne vois pas ou tu veux en venir.

[fatal_error]

Bon je suis allé un peu plus loin dans les calculs, j'ai constaté que j'avais fait une erreur.
Quand je développe, j'arrive à l'égalité ce qui n'est pas très pratique...

[Blisten]

effectivement. tu arrives au même souci que moi. impossible de retirer le sin ou cos pour faire la suite...

[fatal_error]

re, en fouillant un petit peu, je suis tombé sur ce lien


You then divide both sides by :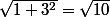 . So, you have:

Now let:
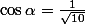, and 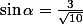. You can do this because you know that:
, so it's true that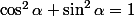
So you have:



la fin diffère un poil mais je pense que ca devrait marcher.

En appliquant à ton cas, j'arrive à

[Blisten]

oki merci bcp je vais voir ce que je peux faire avec ca