Trigonalisation

par **Rik95** » 30 Déc 2015, 19:04

Bonjour,

N'ayant pas pu assister au cours sur la trigonalisation, j'essaye de me rattraper en faisant quelques exercice, j'essaye actuellement de trigonaliser une matrice mais je n'ai pas encore bien saisie la principe, quelqu'un pourrai m'aider svp ?

Voici la matrice en question :

2 -1 -1
2 1 -2
3 -1 -2

Donc je commence par chercher le polynome caractéristique, je trouve : (x-1)²(x+1) donc la matrice est trigonalisable car le polynome est scindé

Ensuite je cherche els espaces propres je trouve les vecteurs : E-1 = ( 1 1 2), E1 = (1 0 1)

A partir de là je coince, j'ai pensais a prendre le vecteur de la base canonique e3 comme 3eme vecteur comme je l'ai vu dans une vidéo mais ai je le droit de faire sa ? ( je ne suis pas sur car ce n'est pas vraiment le même cas que dans la vidéo que j'ai vu ... )

De plus il y'a une chose que je ne comprend pas dans la trigonalisation apparemment la matrice T ( doit sécrire sous la forme :

-1 a b
0 1 b'
0 0 1

Comment puis je calculer le a b et b' ?

Merci

par **Robot** » 30 Déc 2015, 19:11

Si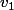

est un vecteur propre de valeur propre associée

,

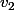un vecteur propre de valeur propre associée

, et que tu complètes avec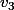

de façon à avoir une base

, quelle tête aura la matrice de l'endomorphisme dans la base

?
Pour faire le calcul, on peut soit faire le changement de base, soit calculer les coordonnées des images de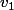

,

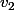et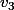

dans la base

(pour les deux premiers, c'est très simple !).

Edit : j'ai corrigé le

en

. L'erreur n'est pas de mon fait, elle est due à un bug de compilation LaTeX sur ce forum : les signes - sans espace devant le mettent en transe et il se met à voir des

partout. J'aurais dû vérifier

par **Rik95** » 30 Déc 2015, 19:25

Robot a écrit:Si est un vecteur propre de valeur propre associée , un vecteur propre de valeur propre associée , et que tu complètes avec de façon à avoir une base , quelle tête aura la matrice de l'endomorphisme dans la base ?
Pour faire le calcul, on peut soit faire le changement de base, soit calculer les coordonnées des images de , et dans la base (pour les deux premiers, c'est très simple !).

Merci pour ta réponse rapide ! mais désolé je ne comprend pas vraiment ce que tu veux dire ?

J'ai deux vecteurs V1 et V2, ainsi que deux valeurs propre x² et 1 et je dois trouver un vecteur V3 ?

Honnêtement je ne vois pas :/

par **MouLou** » 30 Déc 2015, 21:06

Essaye de bien comprendre ce que veux te dire Robot, ce que signifient ses indications, avant de voir ou il veut te mener.

Bon déjà ce sont 1 et -1 les valeurs propres.
tu as déjà trouver les 2 vecteur propres v1 et v2 associées aux valeurs propres 1 et -1.
Si maintentant tu prends un 3e vecteur tel que (v1,v2,v3) est une base quelle est nécéssairement la matrice de l'endomorphisme dans cette nouvelle base?

u(v1)=? (facile)
u(v2)=? (facile)
u(v3)=av1+bv2+cv3 (a,b,c indéterminées).

Que peux tu dire de c?

Conclusion: quel aspect a ta matrice?

par **Rik95** » 30 Déc 2015, 21:48

MouLou a écrit:Essaye de bien comprendre ce que veux te dire Robot, ce que signifient ses indications, avant de voir ou il veut te mener.

Bon déjà ce sont 1 et -1 les valeurs propres.
tu as déjà trouver les 2 vecteur propres v1 et v2 associées aux valeurs propres 1 et -1.
Si maintentant tu prends un 3e vecteur tel que (v1,v2,v3) est une base quelle est nécéssairement la matrice de l'endomorphisme dans cette nouvelle base?

u(v1)=? (facile)
u(v2)=? (facile)
u(v3)=av1+bv2+cv3 (a,b,c indéterminées).

Que peux tu dire de c?

Conclusion: quel aspect a ta matrice?

Si j'ai bien compris, je dirai que U(v1) = (2, 2, 3) transposé, et u(v2) = (-1, 1, -1) transposé , U(v3) = ( 1 -2 -2 ) transposé = av1 +bv2 +cv3, si je prend v3 = e3 je trouve a = -2, b = c = 1

La matrice de passage P est egale a V1, V2, V3 écris en colonne, la matrice T est egal a :

-1 a -2
0 1 1
0 1 1

Si j'ai bien compris le principe la derniere colonne est egale au coeff a, b ,c que j'ai trouvé mais pour le a je ne sais pas, enfin je ne suis meme pas sur de ce que je viens de faire

par **MouLou** » 30 Déc 2015, 21:54

Je ne comprends pas ce que tu racontes. t'as v1=(1,1,2) (le vecteur propre associé à la valeur propre -1) selon tes propres dires, pourquoi tu parles de u (v1)=(2,2,3)?

Pour trigonaliser selon moi, il faut passer à la notion d'endomorphisme. Et ta matrice représente un endomorphisme dans la base canonique. Trigonaliser un endomorphisme revient à donner une base dans laquelle sa matrice est triangulaire.

note bien ceci. (v1,v2,v3) NE SONT PAS les vecteurs de la base canonique, pourquoi veux tu que u(v1)=(2,2,3)? (qui est l'image de e1 dans la base canonique (e1,e2,e3)

Connais tu la notion de Matrice d'un endomorphisme dans une base différente de la base canonique?

par **Rik95** » 30 Déc 2015, 22:06

MouLou a écrit:Je ne comprends pas ce que tu racontes. t'as v1=(1,1,2) (le vecteur propre associé à la valeur propre -1) selon tes propres dires, pourquoi tu parles de u (v1)=(2,2,3)?

Pour trigonaliser selon moi, il faut passer à la notion d'endomorphisme. Et ta matrice représente un endomorphisme dans la base canonique. Trigonaliser un endomorphisme revient à donner une base dans laquelle sa matrice est triangulaire.

note bien ceci. (v1,v2,v3) NE SONT PAS les vecteurs de la base canonique, pourquoi veux tu que u(v1)=(2,2,3)? (qui est l'image de e1 dans la base canonique (e1,e2,e3)

Connais tu la notion de Matrice d'un endomorphisme dans une base différente de la base canonique?

Effectivement ... je n'avais pas bien saisie cette différence au niveau u(v1) et u(v2) mais dans ce cas a quoi sont il egaux ?

J'avoue être complètement perdu

par **MouLou** » 30 Déc 2015, 22:08

Vecteur propre ca veut dire quoi?

par **Robot** » 30 Déc 2015, 22:09

est un vecteur propre pour

, de valeur propre associée

.
Ca veut dire que

par **Rik95** » 30 Déc 2015, 22:19

Robot a écrit: est un vecteur propre pour , de valeur propre associée .
Ca veut dire que

U(v1) = -V1 ?

par **Robot** » 30 Déc 2015, 22:30

Tu n'es pas sûr ?

par **Rik95** » 30 Déc 2015, 22:34

Non, j'ai lu cela dans un pdf que j'ai télécharger mais je ne m'en suis encore jamais servi dans un exercice, en quoi cela aidera a la trigonalisation ?

par **MouLou** » 30 Déc 2015, 22:39

A mon avis tu peux pas trop esperer trigonaliser (ou comprendre comment on trigonalise) une matrice sans savoir ce qu'est un vecteur propre.

Un vecteur propre associé à une valeur propre

, c'est un vecteur non nul qui vérifie

.

Donc la réponse est oui: c'est bien ça.

Même question avec v2. Que vaut u(v2)?

Que peux tu en déduire sur les 2 premières colonnes de la matrice de u dans la base (v1,v2,v3)?

par **Rik95** » 30 Déc 2015, 22:52

MouLou a écrit:A mon avis tu peux pas trop esperer trigonaliser (ou comprendre comment on trigonalise) une matrice sans savoir ce qu'est un vecteur propre.

Un vecteur propre associé à une valeur propre , c'est un vecteur non nul qui vérifie .

Donc la réponse est oui: c'est bien ça.

Même question avec v2. Que vaut u(v2)?

Que peux tu en déduire sur les 2 premières colonnes de la matrice de u dans la base (v1,v2,v3)?

U(v2) = V2

Je dirai que les 2 premières colonnes sont :

-1 0
0 1
0 0

par **MouLou** » 30 Déc 2015, 22:54

Oui! Alors la c'est gagné non?

par **Rik95** » 30 Déc 2015, 23:22

MouLou a écrit:Oui! Alors la c'est gagné non?

Je pense que oui ^^, si j'ai bien compris la suite la derniere colonne est egal au coeff a, b, c de tout a l'heure la matrice est donc :

-1 0 -2
0 1 1
0 0 1

Cependant j'aurai une question dans un autre cas par exemple, pour cette matrice :

-3 -3 2
1 1 -2
2 4 -4

Je trouve comme polynome caractéristique (x+2)^3 il n'y a donc qu'une seule valeur propre -2

Et comme vecteur propre je trouve v1 = (1, -1, -1) donc u(v1) = 2v1

Maintenant pour les vecteurs V2 et V3 j'applique la meme méthode que tout a l'heure ?

V2 = aV1 + bV2 + Cv3 et V3 = a'V1 + b'V2 +c'V3 avec v2 = e2 et v3 = e3 ?

par **Robot** » 31 Déc 2015, 10:13

Quel vecteur as-tu choisi comme

?

Pour l'autre matrice où

est valeur propre de multiplicité 3, ça demande plus de travail. Tu dois d'abord compléter le vecteur propre (base de

) en une base de

.

par **Rik95** » 31 Déc 2015, 17:54

Robot a écrit:Quel vecteur as-tu choisi comme ?

Pour l'autre matrice où est valeur propre de multiplicité 3, ça demande plus de travail. Tu dois d'abord compléter le vecteur propre (base de ) en une base de .

Comme V3 j'ai choisi le vecteur e3 de la base canonique

Pour l'autre matrice je ne comprend pas très bien ce que tu veux dire, la méthode n'est pas la même ?
Pourquoi dois je calculer ker(u +2i)² ?

par **Robot** » 31 Déc 2015, 18:04

Rik95 a écrit:Comme V3 j'ai choisi le vecteur e3 de la base canonique

OK

Rik95 a écrit: Pour l'autre matrice je ne comprend pas très bien ce que tu veux dire, la méthode n'est pas la même ?
Pourquoi dois je calculer ker(u +2i)² ?

Suppose que la matrice de

est triangulaire dans la base

. Montre que

est vecteur propre de valeur propre associée

, c.-à-d.

.

est dans

.

par **Rik95** » 31 Déc 2015, 19:43

Robot a écrit:OK

Suppose que la matrice de est triangulaire dans la base . Montre que
est vecteur propre de valeur propre associée , c.-à-d. .
est dans .

Ok donc si j'ai bien saisie la chose, je calcul w2 de la meme maniere que j'ai calculer w1 mais en calculons (u+2i)²X = 0

puis pour w3 je le calcul de la meme maniere que je l'ai calculer dans l'exercice précédant ?

Trigonalisation

Trigonalisation

Qui est en ligne