Trigo
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 18 Nov 2007, 19:50
par ptitmatteo » 18 Nov 2007, 19:50
pour revenir a lexo d'avant pour on sin(@)=sin(pi-@)
????
-
freud
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Mai 2005, 11:00
-
 par freud » 18 Nov 2007, 20:00
par freud » 18 Nov 2007, 20:00
pour revenir a lexo d'avant pour on sin(@)=sin(pi-@)
????
sin(a+b)=sin(a)cob(b)+sin(b)cos(a) t'appliques cette formule avec a=pi et b=-@
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 18 Nov 2007, 20:04
par ptitmatteo » 18 Nov 2007, 20:04
+i \sin(\pi-\theta)]^8)
donc de
)+i \sin(8\times (\pi-\theta)))
kan je vérifier je ne trouve pas sa??
-
freud
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Mai 2005, 11:00
-
 par freud » 18 Nov 2007, 20:06
par freud » 18 Nov 2007, 20:06
Ha oui et tu verifies comment?
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 18 Nov 2007, 20:08
par ptitmatteo » 18 Nov 2007, 20:08
avec ma calculatrise je fais une résolution et sa me dis faux
-
freud
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Mai 2005, 11:00
-
 par freud » 18 Nov 2007, 20:16
par freud » 18 Nov 2007, 20:16
ptitmatteo a écrit:avec ma calculatrise je fais une résolution et sa me dis faux
essaie, d'utiliser ton cerveau au lieu de ta calculette. Parceque
-cos(a)+isin(a)=cos(pie-a)+isin(pie-a)
et exp(ib)^8=exp(8ib)
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 18 Nov 2007, 20:19
par ptitmatteo » 18 Nov 2007, 20:19
ok merci
en faite il faut utiliser la formule de moivre?
pourl'autre je sus bloquer aussi
z=1+exp^(2@i)
z=cos(0)+i.sin(0)+cos(2@)+sin(2@)
mais aprés je ne sais pas quoi faire??
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 18 Nov 2007, 20:42
par ptitmatteo » 18 Nov 2007, 20:42
???????????????
-
freud
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Mai 2005, 11:00
-
 par freud » 18 Nov 2007, 20:44
par freud » 18 Nov 2007, 20:44
t'as exp(2ipie)+ exp(2ai)
= exp(i(a+pie)*(exp(i(pie-a)+exp(i(a-pie))
=exp(ia)*(exp(-ia)+exp(ia))
=exp(ia)*2cos(a)
.....
-
freud
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Mai 2005, 11:00
-
 par freud » 18 Nov 2007, 20:50
par freud » 18 Nov 2007, 20:50
 par busard_des_roseaux » 18 Nov 2007, 21:15
par busard_des_roseaux » 18 Nov 2007, 21:15
encore un effort, et c'est fini:
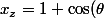 \geq 0)
d'où :
 \in [-\frac{\pi}{2},\frac{\pi}{2}])
quelque soit

d'où si

=\theta)
si

=\theta+\pi)
:dodo: :doh: :doh: :dodo:
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 18 Nov 2007, 21:32
par ptitmatteo » 18 Nov 2007, 21:32
es que tu peut m'expliquer pourquoi
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 18 Nov 2007, 21:39
par xyz1975 » 18 Nov 2007, 21:39
Bonsoir
z=1+exp(2i@)=exp(i@)[exp(-i@)+exp(i@)]=2cos(@).exp(i@).
On ne peut pas dire tout de suite que le module de z est bien 2cos(@) et un argument est @ car la quantité 2cos(@) n'est pas toujours positive. On sépare les cas.
1er cas : Si 2cos(@) est stictement positif
|z|=2cos(@) et arg(z)=@.
2eme cas : Si 2cos(@) est strictement négatif
z=-2cos(@).[-exp(i@)]=-2cos(@).exp(i(@+pi))
|z|=-2cos(@) et arg(z)=@+pi
Dans le cas où 2cos(@)=0 alors z =0 donc son module est nul mais pas d'argument.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
