J'essaie de trouver une équation pour obtenir l'ensemble des temps auxquels se produisent un phénomène physique. Voici un schéma de la situation :
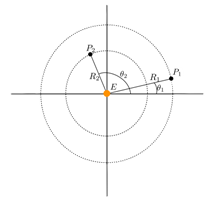
(où P1 et P2 sont des planètes qui gravitent autour de l'étoile E)
Les trajectoires sont considérées comme parfaitement circulaires, les planètes sont soumises à la seconde loi de Kepler.
J'essaie de prédire à quels temps t les planètes sont alignées du point de vue d'un observateur. J'ai déjà réussi à obtenir une équation dans le cas où l'observateur est en O(0,0), mais je dois maintenant obtenir un cas plus général où l'observateur est situé en un point quelconque O(x0, y0).
J'utilise donc la propriété d'un vecteur normal pour dire que :
Pour les vecteurs-rayons
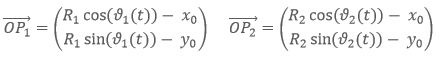
On obtient par définition un vecteur normal à OP1 :
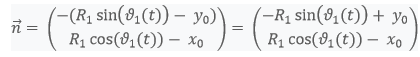
On peut donc poser l'égalité suivante :
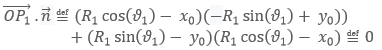
qui laisse une seule condition à vérifier :
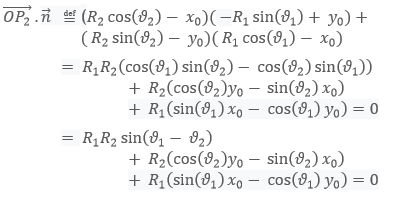
Et je bloque ici, je n'arrive pas à simplifier le calcul. J'essaie d'isoler t tel que :
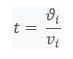
(pour
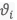l'angle du rayon vecteur par rapport à l'axe des abscisses et 
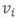la vitesse angulaire de la planète autour de l'étoile)Quelle(s) propriété(s) trigonométrique(s) puis-je utiliser pour me débarrasser de certaines valeurs sin/cos ? De manière générale, est-il toujours possible d'isoler "proprement" t sans obtenir une formule affreuse ?
Merci d'avance pour votre réponse et votre aide, n'hésitez pas à me demander si je n'ai pas été assez clair sur une donnée ou une question.
,