Trigo et complexes.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 27 Oct 2011, 23:37
par Deluxor » 27 Oct 2011, 23:37
Bonsoir,
1) Ecrire sous la forme
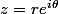
avec
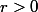
les complexes :
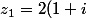^{10})
,
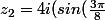+icos(\frac{3\pi}{8})))
,
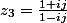
où
 (on pensera à l'"arc moitié" pour écrire
(on pensera à l'"arc moitié" pour écrire  et
et  ...).
...).2) Résoudre dans

l'équation :
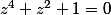
.
---------------------------------
1) Est-ce juste :
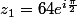
?
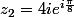
Que faire arrivé là?

-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 27 Oct 2011, 23:40
par Le_chat » 27 Oct 2011, 23:40
Deluxor a écrit: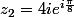
Que faire arrivé là?

Bonsoir. Tu peux dire que i=exp(ipi/2)

-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 28 Oct 2011, 11:06
par Deluxor » 28 Oct 2011, 11:06
Merci Le_chat!
Comment faire concernant
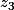
? Je n'ai jamais entendu parler d'"arc moitié"... :/
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 28 Oct 2011, 11:16
par Le_chat » 28 Oct 2011, 11:16
Déjà, tu peux remplacer i par exp(ipi/2) dans ton expression.
Ensuite, la technique de l'arc moitié est la suivante: Au dénominateur tu auras un terme en 1-exp(ia).
Tu peux factoriser par exp(ia/2):1-exp(ia)=exp(ia/2)(exp(-ia/2)-exp(ia/2))
Et comme exp(it)-exp(-it)=2isin(t)...
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 28 Oct 2011, 11:47
par Deluxor » 28 Oct 2011, 11:47
On arrive à :

?
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 28 Oct 2011, 11:50
par Le_chat » 28 Oct 2011, 11:50
Oui je pense que c'est ça! Maintenant factorise par exp(ipi/12)!
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 28 Oct 2011, 11:56
par Deluxor » 28 Oct 2011, 11:56
J'arrive à un truc impossible...
J'ai factorisé :
}{e^{i\frac{\pi}{2}} (e^{-i\frac{\pi}{2}} + e^{i\frac{\pi}{2}}))
Soit :
}{e^{i\frac{\pi}{2}} \times 2 cos(\frac{\pi}{2})})
On arrive à

...

-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 28 Oct 2011, 11:58
par Le_chat » 28 Oct 2011, 11:58
Il faut factoriser par exp(ipi/12), pas exp(ipi/2) :id:
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 28 Oct 2011, 12:01
par Deluxor » 28 Oct 2011, 12:01
En effet!

On arrive donc à :
}{cos(\frac{\pi}{12})})
?
Peut-on "simplifier"?
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 28 Oct 2011, 15:43
par Le_chat » 28 Oct 2011, 15:43
Je ne pense pas que l'on puisse simplifer. Cependant, on te demande la forme trigonometrique de ce nombre, tu saurais la donner? (attention, le "r" est positif!)
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 03 Nov 2011, 18:37
par Deluxor » 03 Nov 2011, 18:37
Je ne trouve pas la forme trigonométrique. Help! ^^
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 03 Nov 2011, 20:40
par Le_chat » 03 Nov 2011, 20:40
Ben cos(pi/12), sin(pi/12) sont des reels, tu dois pas être bien loin du but !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités