Triangle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Chaos
- Membre Naturel
- Messages: 26
- Enregistré le: 05 Fév 2007, 14:03
-
 par Chaos » 27 Fév 2007, 11:08
par Chaos » 27 Fév 2007, 11:08
Bonjour,
Démontrer que si les angles d'un triangle ABC verifient la relation le triangle est rectangle.
sin^2A +sin^2B +sin^2C=2
J'ai transforme sin^2A en sin^2B * cos^2C + sin^2C * cos^2B + 2sinBcosBsinCcosC.
Ensuite j'ai tout reporte dans la relation, mais pi sur 2 n'apparait pas.
-
mathelot
 par mathelot » 27 Fév 2007, 14:11
par mathelot » 27 Fév 2007, 14:11
bonjour,
l'astuce c'est de remarquer que la somme des angles d'un triangle
vaut

, soit
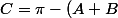)
d'où, après calculs:
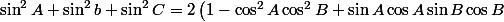)
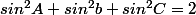
équivaut à:
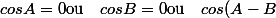=0)
équivaut à:
ABC rectangle.
-
Chaos
- Membre Naturel
- Messages: 26
- Enregistré le: 05 Fév 2007, 14:03
-
 par Chaos » 27 Fév 2007, 14:41
par Chaos » 27 Fév 2007, 14:41
apres calcul je trouve:
2(sin^2B + sin^2C - sin^2C * sin^2B + sinB * cosB * cos C * sinC-1)
Est ce correcte?
-
mathelot
 par mathelot » 27 Fév 2007, 14:59
par mathelot » 27 Fév 2007, 14:59
1) pour vérifier les formules que tu trouves, tu peux tjrs les tester avec
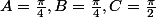
2)
mes ingrédients:
=SIN A COS B + COS A SIN B)
et à un moment:
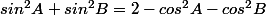
3) mènes tes calculs comme si tu souhaitais factoriser la somme.
-
mathelot
 par mathelot » 27 Fév 2007, 16:28
par mathelot » 27 Fév 2007, 16:28
tu t'en sors Chaos ou k.o ?
-
Chaos
- Membre Naturel
- Messages: 26
- Enregistré le: 05 Fév 2007, 14:03
-
 par Chaos » 27 Fév 2007, 16:49
par Chaos » 27 Fév 2007, 16:49
J'ai des calculs a rallonges........
je trouve pour sin^2B+C
sin^2B + sin^2C - 2sin^2B*sin^C + 2 sinBcosCsinCcosB
Et je reporte tout sa dans la relation:
Et j'obtiens: 2( sin^2B + sin^2C - sin^2B*sin^2C+sinBcosCsinCcosC -1)=0
-
mathelot
 par mathelot » 27 Fév 2007, 17:40
par mathelot » 27 Fév 2007, 17:40
Chaos a écrit:Et j'obtiens: 2( sin^2B + sin^2C - sin^2B*sin^2C+sinBcosCsinCcosC -1)=0
oui, ça s'arrange:
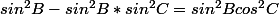
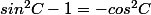
et après tu réduis la somme de ces deux égalités.
-
Chaos
- Membre Naturel
- Messages: 26
- Enregistré le: 05 Fév 2007, 14:03
-
 par Chaos » 27 Fév 2007, 19:11
par Chaos » 27 Fév 2007, 19:11
On trouve: 2(-cos^2B cos^2C+sinBcosCsinCcosB)?????
C'est correcte???
Merci pour les infos
-
mathelot
 par mathelot » 27 Fév 2007, 19:17
par mathelot » 27 Fév 2007, 19:17
Chaos a écrit:On trouve: 2(-cos^2B cos^2C+sinBcosCsinCcosB)?????
C'est correcte???
Merci pour les infos
non, ça ne marche pas pour
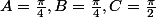
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
