Transposé et orthogonalite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 05 Mai 2007, 17:44
par nemesis » 05 Mai 2007, 17:44
bonjour
pour montrer que
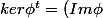^\perp)
je parvien a l'inclusion suivante
^\perp)
est ce qu'il vaut mieux ,pour continuer ,montrer qu'il ont meme dimension ou faire l'inclusion dans l'autre sens
merci d'avance

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 05 Mai 2007, 18:00
par nuage » 05 Mai 2007, 18:00
nemesis a écrit:bonjour
pour montrer que
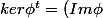^\perp)
je parvien a l'inclusion suivante
^\perp)
est ce qu'il vaut mieux ,pour continuer ,montrer qu'il ont meme dimension ou faire l'inclusion dans l'autre sens
merci d'avance
Si on est en dimension finie n alors :
^\perp)=n-dim (Im\phi) = dim (ker \phi)= dim (ker \phi ^t ))
Théorème du rang.
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 05 Mai 2007, 18:08
par nemesis » 05 Mai 2007, 18:08
oui mais c'est pas en dimension finie
-
adelinou95
- Membre Naturel
- Messages: 13
- Enregistré le: 17 Avr 2007, 11:09
-
 par adelinou95 » 05 Mai 2007, 18:09
par adelinou95 » 05 Mai 2007, 18:09
Pouvez vous m'aidez à résoudre cet exercice sur les probabilités?
Je vous en remercie d 'avance .
Pour un examen,10 examinateurs ont préparé chacun 2 sujets. On dispose donc de 20 sujets que l'on place dans 20 enveloppes identiques.
2 candidats se présentent: chacun choisit au hasard 2 sujets; de plus les sujets choisis par le 1er candidat ne sont plus disponibles pour le 2ème candidat. on note A1 l'évènement:" les 2 sujets obtenus par le premier candidat proviennent du même examinateur" et par A2 l'évènement: "les 2 sujets obtenus par le 2ème candidat proviennent du même examinateur".
1- Calculer la probalité de A1
2- Calculer la probabilité conditionnelle p(A2/A1) de l'évenement A sachant que A1 est réalisé.
Déterminer la probalité que les 2 candidats chacun 2 sujets provenant d'un même examinateur.
3- Calculer la probabilité p(A2/Â1)
Calculer la probalité p(A2) puis en déduire p (A1 U A2)
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 05 Mai 2007, 18:19
par fahr451 » 05 Mai 2007, 18:19
nemesis a écrit:oui mais c'est pas en dimension finie
alors il n y a pas de dimension et ta question précédente n'a pas lieu d'être
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 05 Mai 2007, 18:23
par nemesis » 05 Mai 2007, 18:23
non ce que je veux dire c'est qu'il n'est pas precisé que c'est en dimension finie
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 05 Mai 2007, 18:27
par fahr451 » 05 Mai 2007, 18:27
bon alors
peux tu nous dire de quelle orthogonalité il s'agit?
au sens de la dualité ? au sens des espaces euclidiens?
d'une façon générale donne un énoncé précis qu'est-ce phi ? définie de quoi dans quoi que sont ces quoi ?
-
adelinou95
- Membre Naturel
- Messages: 13
- Enregistré le: 17 Avr 2007, 11:09
-
 par adelinou95 » 05 Mai 2007, 18:33
par adelinou95 » 05 Mai 2007, 18:33
tu ve dire koi par plu maintenan ?
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 05 Mai 2007, 18:49
par nemesis » 05 Mai 2007, 18:49
c'est j'y suis arrivé mais pour ceux que ca interesse :
soit

et

montrer que
^\perp)
bon alors ce que j'ai fait :
=f o \phi =0)
et soit
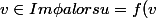 avec v \in E)
on a alors
=f(\phi (v))=fo\phi(v)=0(v)=0)
donc f(u)=0, quelquesoit u dans Im

^\perp donc ker \phi ^t \subset (Im \phi)^\perp)
et pour la deuxeme inclusion j'ai ceci
^\perp)
donc
={0})
alors ona
)(v)=(\psi o \phi)(v)=\psi(\phi(v))=0=0(v))
donc
)(v)=0(v) ,\forall v)
donc
=0)
de plus

donc
^\perp \subset ker \phi^t)
et c'est fini (ouf) j'espère que c'est comprehensible
mais c'est de la deuxieme partie dont je suis pas sure ;que ce que vous en dites ?

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 05 Mai 2007, 18:54
par nuage » 05 Mai 2007, 18:54
Salut, :hum:
adelinou95 a écrit:tu ve dire koi par plu maintenan ?
Je ne sais pas ce que veux dire
far451 mais je ne répondrais certainement pas à quelqu'un, qui, comme toi squatte les sujets d'autres personnes.
Ouvre un nouveau sujet si tu veux une réponse. Et essaye de respecter un minimum ceux qui te lise. En d'autre termes ékri an frenssais.
A+
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 05 Mai 2007, 19:11
par nemesis » 05 Mai 2007, 19:11
alors ,c'est bon ou pas ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 05 Mai 2007, 19:18
par fahr451 » 05 Mai 2007, 19:18
oui "c 'est bon"
entre 19H49 et 20h11 il ne s'est pas écoulé 30min...
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 05 Mai 2007, 19:19
par nemesis » 05 Mai 2007, 19:19
desole ,mais il me fallait ca pour continuer
merci encore
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités