Transitif

[zork]

Bonsoir,

Soit G un groupe opérant sur un ensemble . On suppose que G opère doublement tansitivement sur :

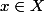
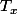
Soit et le stabilisateur de x

Je veux montrer que:
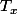
G transitif et transitif sur implique G doublement transitif

Comment faire?

merci

[L.A.]

Bonsoir.

Tu prends des éléments x1,y1,x2,y2, et tu dois construire g qui vérifie deux contraintes.
Tu peux trouver des g1 et g2 satisfaisant chacun l'une des deux contraintes et voir si tu peux les combiner habilement.

[Ben314]

Attention au fait qu'il faut (évidement) que :

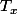
G transitif et, quelque soit x dans G, transitif sur implique G doublement transitif

De plus, "G transitif" me semble un racourçi d'écriture quand même bien abusif...


Aprés il n'y a effectivement qu'a écrire les définitions pour avoir le résultat.