Traduction parce que là...

[package]

Bonjour,

Je m'apperçois de + en +, et je pense que je ne suis pas la seule dans ce cas, que mon problème n'est pas tant de calculer ou apprendre des leçons mais plutôt...de comprendre ce que veulent dire les MOTS!!!

Je vous cite un exemple qui m'empêche d'avancer depuis 1h...

Dire si c'est vrai ou faux :
"Il n'existe pas d'application continue surjective de R sur R-{0}"
Alors bon....euh...QUOI??!!lol..J'ai beau apprendre et essayer de comprendre la définition d'une application surjective, injective etc...mais je comprend toujours pas cette phrase...
Y'aurait-il une traduction TRES explicite pour ce genre d'affirmation, même une explication très très éxagérée même ça me dérangerait pas!!

Voilà j'espère qu'un billingue français/mathématicien pourra m'aider lol...Merci!

[Nightmare]

Bonsoir

Cela veut dire qu'il n'existe pas d'application de R dans R-{0} tel que tout élèment de R-{0} admette au moins un antécédent dans R

En gros on ne peut pas trouver d'application f : R -> R-{0} tel que pour tout y de R-{0} il existe x dans R tel que y=f(x).

En plus gros, Tu ne peux pas trouver de fonction qui nous permette d'associer tout les élèments de R à tout les éléments de R-{0}

[Nuwanda]

Une application, c'est une fonction si tu préfère. Continue, en gros c'est que tu peux tracer la courbe de ta fonction sur un papier sans avoir à lever le crayon. ET surjective, ça veut dire que tout élément de l'espace d'arrivée admet un antécédent par la fonction. Ok ?

[abel]

En gros ca veut dire que si tu prends une fonction de R dans R\{0} continue tu n'as aucune chance qu'elle soit surjective...
Sinon pr comprendre ce que c'est la surjectivité :
Si tu te donnes une valeur quelconque sur l'axe des ordonnées, tu trouveras toujours un (voire plus) antécédent...Bijectif c'est quand on ne trouve qu'un et un seul antécédent.

[package]

Alors encore un ptit problème de français...mais qu'est-ce ça veut dire :
"prendre une fonction de R dans R-{0}" déja?
En gros, ça veut dire une fonction pour laquelle tous les x...euh..non je sais pas.....

[abcd22]

Bonsoir !
C'est une fonction définie sur et telle que pour tout réel . La courbe représentative de la fonction ne coupe pas l'axe des abscisses.

[package]

Yep! Ok si j'ai bien compris "surjectif" et "fonction qui ne passe pas par 0" sont carrément contradictoires...

[abcd22]

La réponse à la question du premier post est bien « vrai », mais je ne sais pas si tu utilises le bon argument : on peut trouver une application surjective de dans 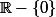: f(x) = x si 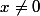et f(0) = 1 par exemple, elle ne prend pas la valeur 0 mais comme 0 n'est pas dans l'espace d'arrivée elle est surjective quand même.

[abel]

Il parlait des fonctions continues.

[abcd22]

Oui, mais en lisant le dernier message de package j'ai eu l'impression qu'elle disait que c'était faux (enfin, que la phrase du premier post était vraie) parce qu'une fonction ne prenant pas la valeur 0 ne peut pas être surjective, c'est pour ça que je fais remarquer que ce n'est pas le bon argument.

[Chimomo]

Cependant package maintenant que tu as compris l'énoncé et que tu sais que la contradiction viens de la continuité tu devrais pouvoir t'en sortir (indication : utiliser un célèbre théorème sur les fonctions continues).

[simplet]

Soit H un p-ss-groupe de G, S un p(Sylow de G. Considérons l'action de H sur G/S=X. (je suppose par conjugaison=automorphisme intérieur).

Comme card(X) est premier à p alors il en est de même pour l'ensemble des points fixes de X par l'action de H (il suffit de prendre la formule des classes) qui est a fortiori non vide.

Ce qui coince vient maintenant:
" Mais alors il existe x dans X tel que H soit inclu dans l'ensemble des points de G qui laissent fixe x." (pourquoi ca??)

Le deuxième truc qui me pose problème c'est pourquoi l'ensemble des points de G qui laissent fixe x est un conjugué de S??



merrccii