Bonjour,
Il y a deux façon de comprendre la questions : soit vous voulez savoir pourquoi "A si B" s'écrit
, soit vous voulez savoir pourquoi on ne dit pas "ssi" dans la définition.
Première option : pourquoi "A si B" s'écrit Dans
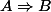
, A est la cause et B est la conséquence : on peut le dire en français par "Si A est vraie alors B est vraie"
Ce qui, toujours en français, est parfaitement identique à "B est vraie si A est vraie".
Au passage :
L'énoncé réciproque est "seulement si" : quand on dit "B est vraie seulement si A est vraie", on en déduit que si B est vraie, nécessairement A est vraie (prendre la contraposée : si A est fausse B ne peut pas être vraie) ; donc ici on a bien
Bref, quand on dit "A si B" cela indique
et quand on dit "A seulement si B" cela indique
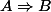
D'où "A ssi B" indique
Seconde option : pourquoi on n'a pas dit "ssi" dans la définitionFormellement c'est bien une équivalence : x est un majorant de A équivaut à dire que tout élément de A est inférieur à x. Mais c'est une équivalence uniquement si on sait ce que c'est qu'un majorant...
Or justement, ici on définit ce qu'est un majorant. Donc ce n'est pas à proprement parler une "proposition mathématique".
Et effectivement une définition "dans l'autre sens" n'aurait pas grand sens : que signifierait en effet la phrase suivante : "on dit que
si x est un majorant de A" sachant qu'on ne sait pas, à ce moment précis, ce qu'est un majorant de A.
C'est valable pour toute définition. "J'appelle cet objet trucmuche s'il vérifie tartempion", cette définition n'a de sens que si on sait ce que c'est que "tartempion" et la définition appellera "Trucmuche" tout ce qui vérifie "tartempion", et uniquement ce qui vérifie "tartempion".
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
